
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основные характеристики системы
Используют следующие основные характеристики системы:
- импульсная функция;
- переходная функция;
- передаточная функция.
Передаточной функцией в изображении по Лапласу называется отношение выходного сигнала к входному.
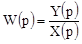 .
.
При определении передаточной функции полиномы y(p) и x(p) могут иметь нулевые корни. Если они имеются в числителе и называются полюсами, то передаточная функция стремится к нулю. Это означает, что система не реагирует на входной сигнал. По отношению к фильтрам, это означает, что фильтр не пропускает соответствующую частоту. Если нули находятся в знаменателе, то это означает, что гипотетически значение передаточной функции стремится к бесконечности. Отсюда следует то, что система является неустойчивой. Для определения устойчивости системы используем анализ характеристического уравнения, которое получают приравниванием знаменателя к нулю:
b0+ b1p+b2p2+… +bm pm=0.
Решая это уравнение, мы получаем m-корней комплексного переменного
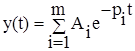 ,
,
где pi – корень характеристического уравнения.
В зависимости от значений действительной и мнимой части корней p=a±jb получаются различные переходные процессы(см.рис.5.10, 5.13, 5.14).
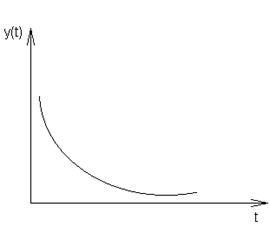
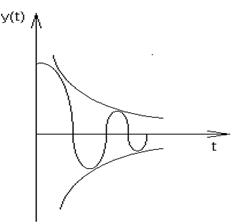
Рис.5.10. a>0, b>0 Рис.5.11. a>0, b¹0
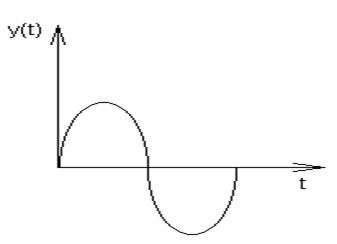
Рис.5.12. Устойчивый синусоидальный сигнал. a=0, b¹0
1. Неустойчивый переходный процесс, возрастающий по экспоненциальному закону.
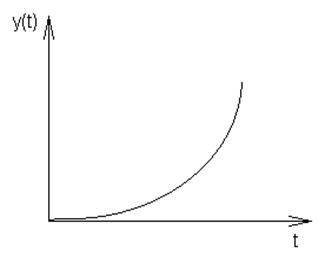
Рис.5.13. a<0, b=0
2. Неустойчивый расходящийся процесс с огибающими по экспоненциальной зависимости
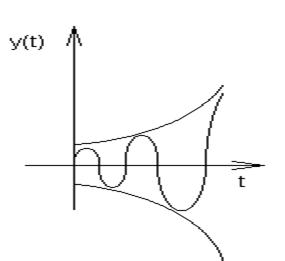
Рис. 5.14. a<0, b¹0
5.4 Расчет электрических цепей
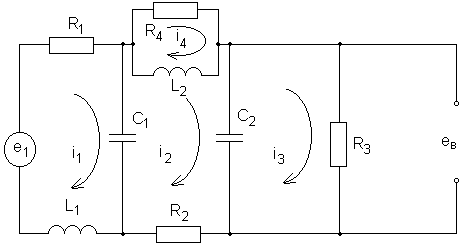 |
Пусть дана схема (рис.5.15)
Рис 5.15. Электрическая схема
е1 – входное напряжение;
ев – выходное напряжение;
i1, i2, i3, i4 – токи соответствующих контуров.
Поскольку передаточная функция
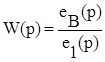
зависит только от параметров цепи L, C, R, то эта передаточная функция может быть определена на основе решения системы дифференциальных уравнений относительно контурных токов.
Система дифференциальных уравнений может быть составлена на одном из законов расчёта электрических цепей, в том числе законов Кирхгофа, метода узловых потенциалов и метода контурных токов.
1. Составим интегро-дифференциальные уравнения по методу контурных токов:
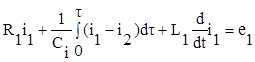 ,
, 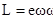
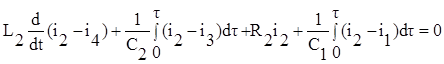 ,
,
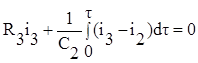 ,
,
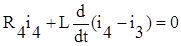 ,
,
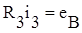 .
.
2. Переходим с помощью преобразований Лапласа к изображению этих уравнений в области комплексного переменного.
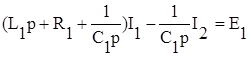
где p – комплексная переменная
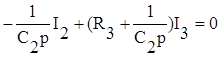
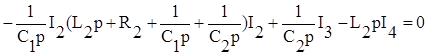
.
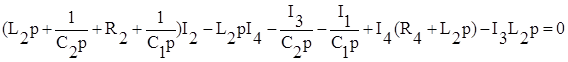
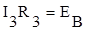 .
.
3.Решаем эти уравнения относительно токов, далее найдем выходное напряжение через ток I3, входное – через ток I1, затем найдем передаточную функцию.
Более подробно этапы расчетов электрических цепей приведены в методических указаниях [10,11]
5.5 Вопросы для самоконтроля
1. Основные понятия при моделировании электрических цепей.
2. Особенности функций с временным аргументом.
3. Особенности функций с частотным аргументом.
4. Особенности функций с комплексным аргументом.
5. Назначение и свойства прямого и обратного преобразования Фурье.
6. Назначение и свойство прямого и обратного преобразования Лапласа.
7. Перечислите основные характеристики систем.
8. Что такое устойчивость систем?
9. Как определить устойчивость систем по передаточной функции?
10. Можно ли определить АЧХ и ФЧХ по передаточной функции?
| <== предыдущая страница | | | следующая страница ==> |
| Преобразования Фурье и Лапласа | | | ЧИСЛЕННЫЕ МЕТОДЫ. Задачи математического моделирования тесно связаны с задачами решения различных уравнений или систем уравнений |
Дата добавления: 2014-08-04; просмотров: 322; Нарушение авторских прав

Мы поможем в написании ваших работ!