V. АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД И МАССИВОВ. ОСНОВНЫЕ ФАКТОРЫ, ВЛИЯЮЩИЕ НА АКУСТИЧЕСКИЕ СВОЙСТВА ГОРНЫХ ПОРОД

Характер распространения упругих колебаний в горных породах определяется акустическими параметрами пород. К ним относятся скорости распространения упругих волн, коэффициенты поглощения, отражения и преломления и волновое сопротивление.

Под скоростью волны понимают скорость распространения некоторой фазы упругих колебаний.

Скорость распространения упругих волн в абсолютно упругой изотопной среде определяется по следующим формулам теории упругости:

Скорость продольной упругой волны в массиве

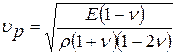, м/с (5.1)

Если 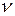= 0,25, ≈ 1,1 ,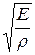

Скорость распространения поперечной упругой волны

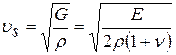, м/с (5.2)

Если 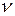= 0,25, то 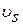≈ 0,63 ,

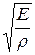Скорость распространения поверхностной упругой волны

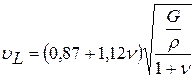, (5.3)

Если 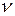= 0,25, то 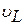= 0,92 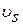≈ 0,58 .

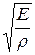При этом всегда соблюдается следующее соотношение скоростей: > >

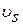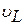
Скорость распространения продольной упругой волны в тонкой пластине породы

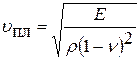, (5.4)

Если 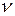= 0,25, 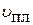≈ 1,33 .

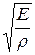Скорость распространения упругой волны в тонком стержне породы

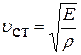, (5.5)

Скорость распространения упругих волн в горных породах определяется их упругими свойствами и плотностью.

Отношение скоростей продольных и поперечных волн является функцией коэффициента Пуассона.

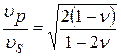, (5.6)

С увеличением модуля Юнга и коэффициента Пуассона возрастает скорость распространения продольной упругой волны. Скорость распространения поперечной волны увеличивается с увеличением Е и уменьшается с увеличением коэффициента Пуассона.

Распространение упругих волн в горных породах, так же как и в любом веществе сопровождается постепенным уменьшением их интенсивности (амплитуды) по мере удаления от источника излучения.

Интенсивность колебаний в большинстве случаев уменьшается по следующим причинам:

1. поглощение части энергии упругих колебаний породой и превращение ее в тепловую, обусловленную взаимным трением частиц породы, совершающих колебательные движения;

2. рассеивание акустической энергии на неоднородностях породы (порах, трещинах, вкраплениях и т.д.).

Амплитуда упругих колебаний И, характеризующая интенсивность колебаний, связана с пройденным волной расстоянием X экспоненциальной зависимостью

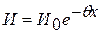, (5.7)

где 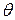– коэффициент поглощения, м^-1.

Коэффициент поглощения зависит как от свойств породы, так и от частоты колебаний f. Для большинства пород зависимость 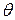от f линейная. В глинистых породах коэффициент 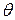пропорционален .

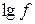Породы обладают сопротивлением распространению в них упругих волн, которое оценивается удельным волновым сопротивлением (акустической жесткостью) горной породы. Акустическая жесткость в сущности является отношением давления волны 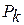мгновенной скорости колеблющихся частиц :

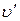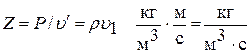, (5.8)

Единица 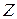называется акустическим Омом.

Удельное волновое сопротивление пород определяет их способность отражать и преломлять упругие волны. Отражение и преломление происходит либо на границе между породами с различными акустическими параметрами, либо при переходе упругих волн из внешней среды в породу (и наоборот).

К преломлению и отражению упругих волн можно применить законы геометрической оптики.

Коэффициентом отражения называется отношение энергии отраженной волны 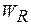к энергии падающей волны 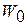. При этом углы падения 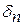и отражения 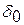звуковой волны от границы раздела равны (рис. 5.2)

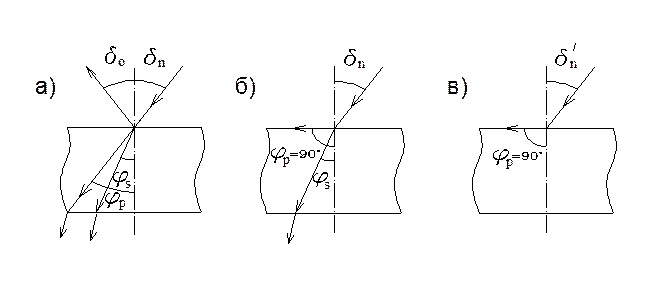Рис. 5.2. Преломление и отражение ультразвуковой волны на границе раздела двух сред:

а) общий случай; б) момент внутреннего отражения продольной волны; в) момент внутреннего отражения поперечной волны; 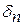и 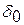– углы падения и отражения; 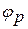и – углы преломления продольной и поперечной волны.

Коэффициент при нормальном падении волны можно выразить также через удельное волновое сопротивление – чем больше разница в волновых сопротивлениях сред, тем больше отражается энергии:

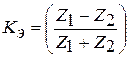, (5.9)

Угол падения 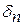и угол преломления 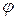упругой волны, проникшей в горную породу, подчиняется закону Снеллиуса, согласно которого углы находятся в определенном соотношении со скоростями упругой волны в первой 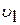и второй 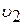средах:

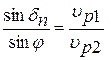, (5.10)

Отношение 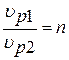– называется коэффициентом преломления упругой волны относительно первой среды.

Больше колебания акустических свойств горных пород объясняются значительным разнообразием минерального состава, структуры, текстуры и влажности.

Увеличение плотности пород сопровождается ростом скорости распространения в них упругих волн и снижением потерь волновой энергии. Влияние основных внутренних и внешних факторов на скорости распространения упругих волн в горных породах приведены на рис. 5.3-5.7.

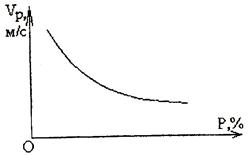
Рис. 5.3. Зависимость скорости Рис. 5.4. Зависимость скорости

продольной волны от продольной волны от

объемной массы пористости

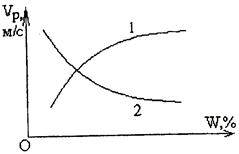
Рис. 5.5. Зависимость скорости Рис. 5.6. Зависимость скорости

продольной волны продольной волны от

породах от напряжений s влажности W: 1 – неразмокаемые

породы; 2 – размокаемые породы

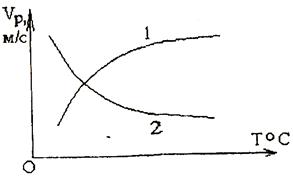
Рис. 5.7. Зависимость скорости продольной волны от температуры Т: 1 – породы, уплотнение которых происходит при нагревании; 2 – породы, ослабление которых происходит при нагревании

В слоистых породах скорость упругих волн вдоль и поперек слоев различна, причем всегда 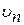> 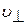. Если порода состоит из слоев 2-х типов, то скорость упругих волн перпендикулярно слоям в простейшем случае при их равных удельных волновых сопротивлениях может быть вычислена по суммарному времени прохождения волн через все слои.

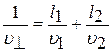, (5.11)

где 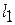– относительные толщины слоев со скоростью звука соответственно 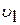и .

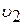Скорость звука при тех же условиях

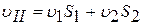, (5.12)

где 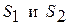– площадь слоев в поперечном сечении.

Отношение скоростей упругих волн вдоль и поперек слоистости породы характеризуется коэффициентом анизотропии.

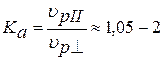. (5.13)

Дата добавления: 2014-05-04; просмотров: 1680; Нарушение авторских прав

Мы поможем в написании ваших работ!