
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Преобразования Фурье и Лапласа
Для перехода из временной области в частотную используются прямое и обратное преобразования Фурье следующего вида:
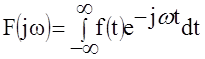 ;
;
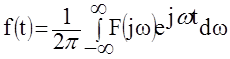 ,
,
где f(t), F(jw) – соответственно функция от времени и функция от частоты.
Формула имеет место для непрерывных преобразований периодических функций на бесконечном временном и частотном интервалах.
В вычислительных процедурах и прикладных задачах используются дискретные представления прямого и обратного преобразования Фурье, которое получаются из непрерывного представления функций заменой интеграла на сумму
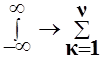 ,
,
ограниченную конечным рядом элементов.
При этом 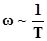 . K – индекс суммы - пробегает значения по дискретным временным отчётам либо по дискретным частотным отчётам. Ниже приведены графики функций временного и частотного аргумента.
. K – индекс суммы - пробегает значения по дискретным временным отчётам либо по дискретным частотным отчётам. Ниже приведены графики функций временного и частотного аргумента.
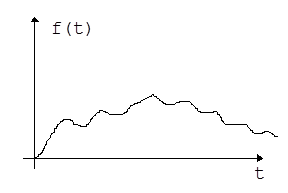
Рис. 5.5.Функция временного аргумента
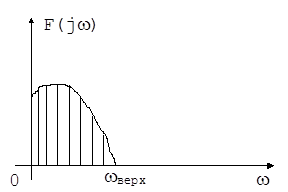
Рис. 5.6. Функция частотного аргумента
Частотные представления показывают распределение энергии сигнала по соответствующим частотам.
Множитель eхр (экспонента) играет роль масштабирующего коэффициента в преобразовании Фурье. Его можно заменить суммой функций sin и cos:
cos wt - j sin wt = e - jwt,;
где sin, cos - позволяет показать функцию в комплексной области (рис.5.7, 5.8), 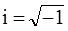 - мнимая единица.
- мнимая единица.
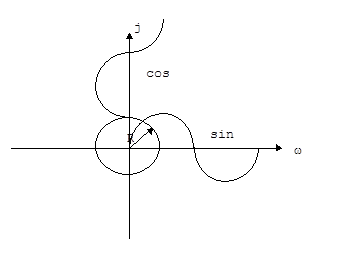
Рис. 5.7.Представление функции в комплексной области
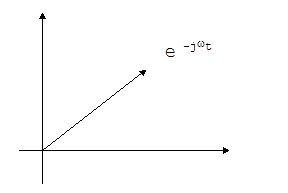
Рис. 5.8.Представление точки в комплексной области
В вычислительной технике используется дискретное время и дискретная частота.
Пусть t - дискретное время при постоянном шаге дискретизации.
t = D = t2 - t1;
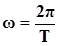 ;
;
T=kt ;
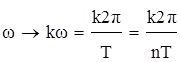 ;
;
где k - текущий дискретный индекс по частоте;
n - текущий дискретный индекс по времени.
Функции, представленные в дискретном виде, называют решетчатыми.
Так как преобразование Фурье связывает временные и частотные области с представлением в комплексной плоскости, то возникает возможность формальной замены jw на комплексное число p = a + jb
Для преобразования временного сигнала в комплексную область используются преобразования по Лапласу:
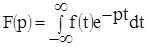 ,
,
где p - комплексное число
F (p) - изображение функции по Лапласу.
Обратное преобразование по Лапласу имеет вид:
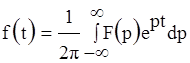 .
.
Для работы в вычислительной среде используют прямое и обратное представление Лапласа, где интеграл заменяется суммой, а соответствующие элементы - дискретными отчётами.
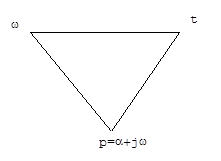
Рис.5.9.Треугольник аргументов
При использовании преобразования Лапласа считают, что в системе отсутствуют возмущения, то есть на момент t0 никаких остаточных переходов не наблюдается и воздействует только входной сигнал. Если взять при высказанных ограничениях от дифференциального уравнения и, используя свойства аддитивности интеграла, применить преобразования Лапласа к каждому элементу дифференциального уравнения то, можно перейти к следующей формуле
a0y(p)+ a1py(p)+… +an pn y(p)= b0x(p)+ b1px(p)+…+ bm pm x(p).
То есть переход от дифференциального уравнения к алгебраическому можно свести к замене:
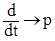
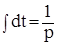 ;
;
x(p)=(a0+ a1p+… +an pn) ;
y(p)=(b0+ b1p+… +bm pm);
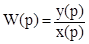 ,
,
где W(p) - передаточная функция, т.е. отношение выходного сигала к входному в изображениях по Лапласу при нулевых начальных условиях. Последнее обозначает, что в системе нет остаточных процессов. Коэффициенты a и b полностью определяются структурой системы (зависят от R, C, L, 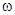 ¾ электрических элементов цепи и частоты w ).
¾ электрических элементов цепи и частоты w ).
В исследовании электротехнических систем различают три задачи, в зависимости от заданных характеристик:
1. Определяем отклик (от структурной функции системы) - получение определенного сигнала y(p) на выходе системы:
y(p)=W(p)×x(p) .
2. Определяем входное воздействие X(p):
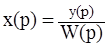 .
.
3. Определяем передаточную функцию по выходному и входному воздействию:
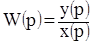 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Моделирование электрических СИСТЕМ | | | Основные характеристики системы |
Дата добавления: 2014-08-04; просмотров: 650; Нарушение авторских прав

Мы поможем в написании ваших работ!