
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Локальная теорема Муавра-Лапласа
Поэтому, когда число испытаний велико, для вычисления вероятности Pm,n(A) применять формулу Бернулли нецелесообразно. Нужны формулы, по которым достаточно точные значения вероятностей Pm,n (A) находились бы при сравнительно несложных вычислениях. Такими формулами являются формулы Муавра - Лапласа и Пуассона. Эти формулы являются асимптотическими.
Теорема. Если вероятность наступления события А в каждом из n испытаний постоянна и равна р, причем отлична от нуля и единицы, а число испытаний достаточно велико, то вероятность Pm,n (A) того, что при n независимых испытаниях событие А наступит m раз, приближенно равна: 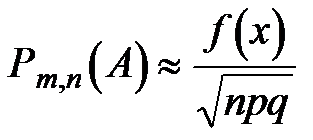 ,где функция
,где функция 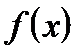 определяется равенством
определяется равенством  ,
, 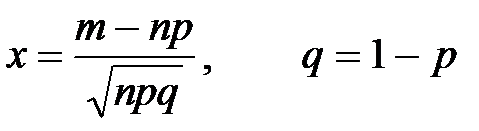 .
.
Теорему рассмотрим без доказательства, так как строгое доказательство ее выходит за рамки математического аппарата, который положен в основу настоящего пособия.
Итак, 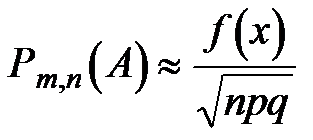 , где
, где 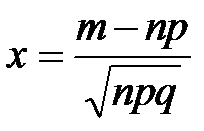 .
.
С возрастанием n относительная точность вычисления вероятностей 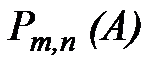 , получаемых по формуле Муавра - Лапласа, возрастает. Если выполняется условие
, получаемых по формуле Муавра - Лапласа, возрастает. Если выполняется условие 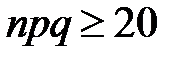 , то вычисления по рассматриваемой формуле дают приемлемую точность.
, то вычисления по рассматриваемой формуле дают приемлемую точность.
Для упрощения расчетов 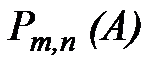 по формуле Муавра - Лапласа составлена таблица значений функции
по формуле Муавра - Лапласа составлена таблица значений функции  (прил. 1). Пользуясь данной таблицей, необходимо иметь в виду свойства этой функции, а именно:
(прил. 1). Пользуясь данной таблицей, необходимо иметь в виду свойства этой функции, а именно:
1) функция  - четная, то есть
- четная, то есть  . Поэтому в таблице приведены значения функции только для положительных значений аргумента;
. Поэтому в таблице приведены значения функции только для положительных значений аргумента;
2) функция  - монотонно убывающая при положительных значениях х. Уже при х=5
- монотонно убывающая при положительных значениях х. Уже при х=5 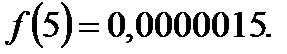 Следовательно, при
Следовательно, при  можно считать, что
можно считать, что 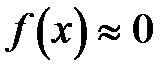 . Поэтому таблица значений функции
. Поэтому таблица значений функции  приводится только для
приводится только для 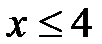 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Теорема Пуассона | | | Конструкторский раздел |
Дата добавления: 2014-09-01; просмотров: 559; Нарушение авторских прав

Мы поможем в написании ваших работ!