Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 2. Напряженность электрического поля. Принцип суперпозиции. Теорема Гаусса
1. Напряженность электрического поля. Напряженностью электрического поля в заданной точке называется физическая величина, равная отношению силы, с которой электрическое поле действует на точечное тело с положительным электрическим зарядом, помещенным в данную точку поля, к этому заряду.
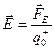 (2.1) – математическая запись определения напряженности электрического поля в заданной точке. В формуле (2.1)
(2.1) – математическая запись определения напряженности электрического поля в заданной точке. В формуле (2.1) 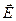 - напряженность электрического поля в заданной точке,
- напряженность электрического поля в заданной точке, 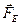 - сила, с которой электрическое поле действует на точечное тело с положительным электрическим зарядом
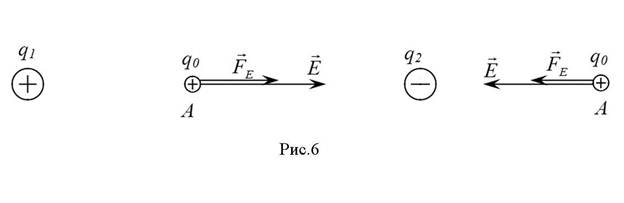
- сила, с которой электрическое поле действует на точечное тело с положительным электрическим зарядом 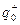 , помещенное в заданную точку (электрическая сила). Из определения (2.1) следует, что
, помещенное в заданную точку (электрическая сила). Из определения (2.1) следует, что  (рис.6).
(рис.6).
 |
Из определения (2.1) 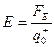 (2.2), где Е – модуль напряженности электрического поля в заданной точке, FE – модуль электрической силы.
(2.2), где Е – модуль напряженности электрического поля в заданной точке, FE – модуль электрической силы.
Получим формулу для вычисления напряженности электрического поля точечного тела с электрическим зарядом в заданной точке.
|
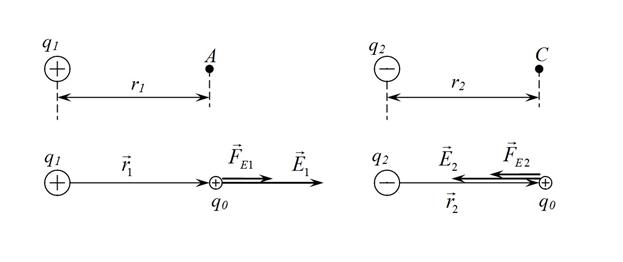
 В соответствии с определением (2.1) поместим в т.А точечное тело с положительным электрическим зарядом
В соответствии с определением (2.1) поместим в т.А точечное тело с положительным электрическим зарядом 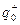 (рис.7) и для взаимодействия точечных тел с электрическими зарядами
(рис.7) и для взаимодействия точечных тел с электрическими зарядами 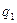 и
и 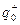 запишем закон Кулона:
запишем закон Кулона:
|
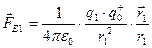 .
. 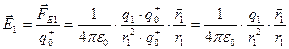 .
.
 В точке А напряженность электрического поля
В точке А напряженность электрического поля 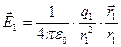 , вектор
, вектор 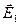 лежит на прямой, соединяющей точечное тело с электрическим зарядом q1 с т.А и направлен от этого точечного тела. Аналогично получаем формулу для напряженности электрического поля в т.С:
лежит на прямой, соединяющей точечное тело с электрическим зарядом q1 с т.А и направлен от этого точечного тела. Аналогично получаем формулу для напряженности электрического поля в т.С: 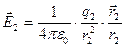 . Так как q2 < 0, то
. Так как q2 < 0, то 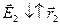 , то есть вектор
, то есть вектор 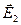 лежит на прямой, соединяющей точечное тело с электрическим зарядом q2 с т.С и направлен к этому точечному телу. В общем случае
лежит на прямой, соединяющей точечное тело с электрическим зарядом q2 с т.С и направлен к этому точечному телу. В общем случае 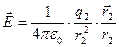 (2.3). В формуле (2.3) q – электрический заряд точечного тела,
(2.3). В формуле (2.3) q – электрический заряд точечного тела, 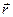 – радиус-вектор, проведенный из точечного тела в заданную точку,
– радиус-вектор, проведенный из точечного тела в заданную точку,
r – модуль этого радиус-вектора (расстояние от точечного тела до заданной точки), 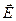 - напряженность электрического поля в заданной точке. Из (2.3) получаем формулу для модуля напряженности электрического поля точечного тела с электрическим зарядом в заданной точке:
- напряженность электрического поля в заданной точке. Из (2.3) получаем формулу для модуля напряженности электрического поля точечного тела с электрическим зарядом в заданной точке: 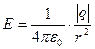 (2.4),
(2.4), 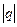 – модуль электрического заряда точечного тела.
– модуль электрического заряда точечного тела. 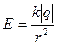 – вариант записи формулы (2.4). Модуль напряженности электрического поля точечного тела с электрическим зарядом в заданной точке обратно пропорционален квадрату расстояния от точечного тела до заданной точки. На рис.8 представлен график этой зависимости.
– вариант записи формулы (2.4). Модуль напряженности электрического поля точечного тела с электрическим зарядом в заданной точке обратно пропорционален квадрату расстояния от точечного тела до заданной точки. На рис.8 представлен график этой зависимости.
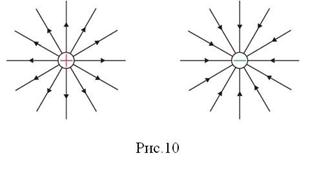
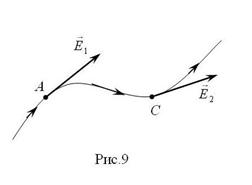
Силовой линией электрического поля называется линия с указанным на ней направлением, в каждой точке которой напряженность электрического поля является касательной к этой линии и направление напряженности совпадает с направлением на малом участке силовой линии, содержащем точку касания (рис.9). Силовые линии электрических полей точечных тел с электрическими зарядами изображены на рис.10.
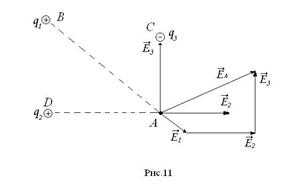 2. Принцип суперпозиции. Для любой точки Аi в некотором объеме V напряженность электрического поля нескольких тел с электрическими зарядами, расположенных в этом объеме, равна сумме напряженностей электрических полей в этой точке, которые были бы при отдельном поочередном расположении в этом объеме каждого из тел при условии, что расположение каждого тела идентично его первоначальному расположению в объеме V вместе с другими телами. Это утверждение называется принципом суперпозиции. На рис.11 показано применение принципа суперпозиции для электрического поля трех точечных тел с электрическими зарядами q1, q2 и q3.
2. Принцип суперпозиции. Для любой точки Аi в некотором объеме V напряженность электрического поля нескольких тел с электрическими зарядами, расположенных в этом объеме, равна сумме напряженностей электрических полей в этой точке, которые были бы при отдельном поочередном расположении в этом объеме каждого из тел при условии, что расположение каждого тела идентично его первоначальному расположению в объеме V вместе с другими телами. Это утверждение называется принципом суперпозиции. На рис.11 показано применение принципа суперпозиции для электрического поля трех точечных тел с электрическими зарядами q1, q2 и q3. 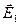 ,
,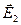 и
и 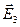 - напряженности электрических полей в т.А, которые были бы, если бы точечные тела с электрическими зарядами q1, q2 и q3 располагались в точках В, С и D по одному поочередно.
- напряженности электрических полей в т.А, которые были бы, если бы точечные тела с электрическими зарядами q1, q2 и q3 располагались в точках В, С и D по одному поочередно. 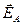 - напряженность электрического поля в т.А при одновременном расположении точечных тел в точках В, С и D. В соответствии с принципом суперпозиции
- напряженность электрического поля в т.А при одновременном расположении точечных тел в точках В, С и D. В соответствии с принципом суперпозиции 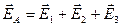 . Формулу для модуля
. Формулу для модуля 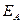 можно получить из этого равенства, применяя соответствующие математические теоремы и определения.
можно получить из этого равенства, применяя соответствующие математические теоремы и определения.
 Определив направление вектора
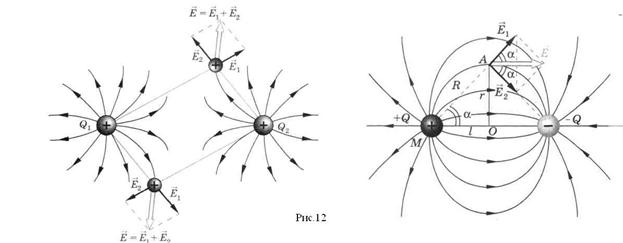
Определив направление вектора 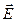 во многих точках электрического поля, можно построить силовые линии электрического поля нескольких точечных тел с электрическими зарядами. На рис.12 изображены силовые линии электрического поля двух точечных тел с электрическими зарядами.
во многих точках электрического поля, можно построить силовые линии электрического поля нескольких точечных тел с электрическими зарядами. На рис.12 изображены силовые линии электрического поля двух точечных тел с электрическими зарядами.
В настоящее время для вычерчивания силовых линий электрического поля нескольких тел с электрическими зарядами успешно используются компьютерные программы.
|
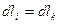 . Середины этих элементов являются концами диаметра кольца. Расстояния b от
. Середины этих элементов являются концами диаметра кольца. Расстояния b от 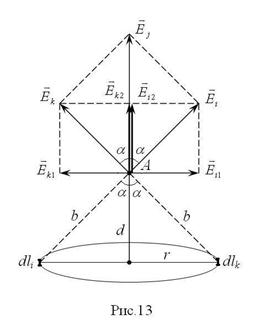 любого элемента с длиной
любого элемента с длиной 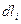 до т.А одинаковы:
до т.А одинаковы: 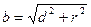 (2.5) Электрический заряд каждого элемента
(2.5) Электрический заряд каждого элемента 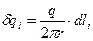 (2.6).
(2.6).
Элемент 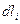 с электрическим зарядом
с электрическим зарядом 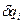 является точечным телом. Модуль напряженности электрического поля элемента кольца с электрическим зарядом
является точечным телом. Модуль напряженности электрического поля элемента кольца с электрическим зарядом 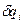 в т.А в соответствии с формулой (2.4)
в т.А в соответствии с формулой (2.4)
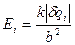 (2.7). Подставляя формулы (2.5) и (2.6) в (2.7), получаем
(2.7). Подставляя формулы (2.5) и (2.6) в (2.7), получаем 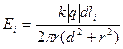 (2.8). Из (2.8) видно, что для всех элементов кольца модули
(2.8). Из (2.8) видно, что для всех элементов кольца модули 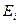 одинаковы. В частности,
одинаковы. В частности, 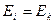 . В соответствии с принципом суперпозиции
. В соответствии с принципом суперпозиции 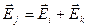 .
. 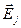 - напряженность электрического поля двух диаметрально противоположных элементов кольца с электрическими зарядами
- напряженность электрического поля двух диаметрально противоположных элементов кольца с электрическими зарядами 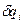 в точке А. Векторы
в точке А. Векторы 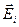 и
и 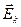 представим в виде суммы двух слагаемых:
представим в виде суммы двух слагаемых: 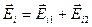 ,
, 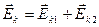 . С учетом этих равенств
. С учетом этих равенств 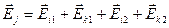 (2.9). В равенстве (2.9) слагаемые
(2.9). В равенстве (2.9) слагаемые 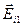 и
и 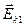 параллельны плоскости кольца, слагаемые
параллельны плоскости кольца, слагаемые 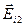 и
и 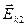 перпендикулярны этой плоскости.
перпендикулярны этой плоскости. 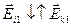 ,
, 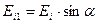 ,
, 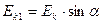 , то есть
, то есть 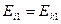 . Это значит, что
. Это значит, что 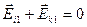 , и (2.9) преобразуется в равенство
, и (2.9) преобразуется в равенство 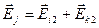 (2.10).
(2.10). 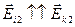 ,
, 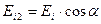 (2.11)
(2.11) 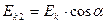 , то есть
, то есть 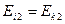 . Это значит, что
. Это значит, что 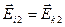 и (2.10) преобразуется в равенство
и (2.10) преобразуется в равенство 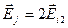 . Из этого равенства следует, что
. Из этого равенства следует, что 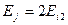 . С учетом (2.8) и (2.11) из этого равенства получаем
. С учетом (2.8) и (2.11) из этого равенства получаем 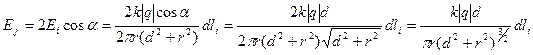
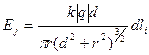 - формула для модуля напряженности электрического поля двух диаметрально противоположных элементов кольца с электрическими зарядами
- формула для модуля напряженности электрического поля двух диаметрально противоположных элементов кольца с электрическими зарядами 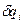 в заданной точке А.
в заданной точке А.
В соответствии с принципом суперпозиции  . Так как все
. Так как все 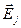 сонаправлены, то
сонаправлены, то 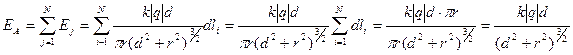
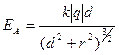 (2.12) - формула для модуля напряженности электрического поля тонкого кольца радиусом r с равномерно распределенным зарядом q в точке А на оси кольца на расстоянии d от плоскости кольца.
(2.12) - формула для модуля напряженности электрического поля тонкого кольца радиусом r с равномерно распределенным зарядом q в точке А на оси кольца на расстоянии d от плоскости кольца.
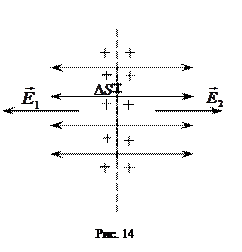 Рассмотрим электрическое поле бесконечно протяженной плоскости с электрическим зарядом, непрерывно распределенным по этой плоскости.
Рассмотрим электрическое поле бесконечно протяженной плоскости с электрическим зарядом, непрерывно распределенным по этой плоскости.
Физическая величина, равная отношению электрического заряда 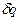 на поверхности с малой площадью
на поверхности с малой площадью 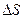 к этому заряду, называется поверхностной плотностью электрического заряда:
к этому заряду, называется поверхностной плотностью электрического заряда: 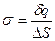 (2.13) – математическая запись определения поверхностной плотности электрического заряда. Если
(2.13) – математическая запись определения поверхностной плотности электрического заряда. Если 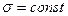 для всех точек плоскости, то векторы
для всех точек плоскости, то векторы 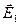 и
и 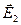 перпендикулярны плоскости,
перпендикулярны плоскости, 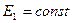 ,
, 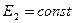 . Электрическое поле является однородным и по одну сторону от плоскости, и по другую сторону от нее. Силовыми линиями такого поля являются прямые, перпендикулярные плоскости (рис.14). Эти выводы можно сделать, разбив плоскость на бесконечное множество поверхностей с малыми
. Электрическое поле является однородным и по одну сторону от плоскости, и по другую сторону от нее. Силовыми линиями такого поля являются прямые, перпендикулярные плоскости (рис.14). Эти выводы можно сделать, разбив плоскость на бесконечное множество поверхностей с малыми 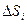 и используя для системы из множества точечных тел с электрическими зарядами
и используя для системы из множества точечных тел с электрическими зарядами 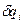 принцип суперпозиции.
принцип суперпозиции.
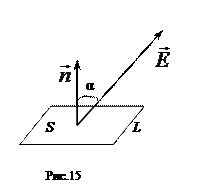 3. Поток напряженности электрического поля. Теорема Гаусса. Потоком вектора
3. Поток напряженности электрического поля. Теорема Гаусса. Потоком вектора 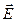 через плоскую поверхность с площадью S, ограниченную замкнутым контуром L, называется физическая величина, равная произведению модуля напряженности электрического поля Е на площадь плоской поверхности S и на косинус угла между вектором
через плоскую поверхность с площадью S, ограниченную замкнутым контуром L, называется физическая величина, равная произведению модуля напряженности электрического поля Е на площадь плоской поверхности S и на косинус угла между вектором 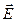 и нормалью
и нормалью 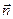 к плоской поверхности (рис.15).
к плоской поверхности (рис.15). 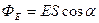 - математическая запись определения потока вектора
- математическая запись определения потока вектора 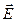 через плоскую поверхность. Так как
через плоскую поверхность. Так как 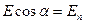 , то
, то 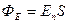 (2.14), где
(2.14), где 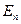 - проекция вектора
- проекция вектора 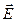 на нормаль
на нормаль 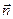 . Определение (2.14) правомерно только в однородном электрическом поле.
. Определение (2.14) правомерно только в однородном электрическом поле.
Если поверхность с площадью S неплоская, либо электрическое поле неоднородное, либо то и другое вместе, то в этих случаях можно дать определение потока вектора 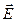 через поверхность с малой площадью dS.
через поверхность с малой площадью dS. 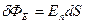 (2.15). В определении (2.15)
(2.15). В определении (2.15) 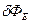 - поток вектора
- поток вектора 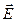 через поверхность с малой площадью dS. Площадь поверхности dS можно считать малой, если во всех точках поверхности
через поверхность с малой площадью dS. Площадь поверхности dS можно считать малой, если во всех точках поверхности 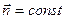 и
и 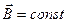 . Величина
. Величина 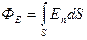 (2.16) называется потоком вектора
(2.16) называется потоком вектора 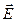 через поверхность произвольной формы, ограниченную замкнутым контуром L и расположенную в неоднородном электрическом поле (рис.16). Поток ФЕ можно вычислить, если проекция Еn задана как функция координат Еn(x,y,z) на всей поверхности с площадью S.
через поверхность произвольной формы, ограниченную замкнутым контуром L и расположенную в неоднородном электрическом поле (рис.16). Поток ФЕ можно вычислить, если проекция Еn задана как функция координат Еn(x,y,z) на всей поверхности с площадью S.
|
| |
|
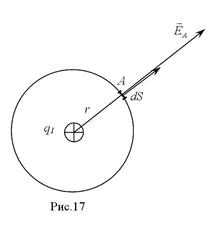
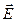 через эту поверхность (рис.17).
через эту поверхность (рис.17).
|
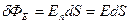 (2.17) - поток вектора
(2.17) - поток вектора 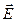 через малую часть сферической поверхности с малой площадью dS.
через малую часть сферической поверхности с малой площадью dS. 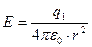 (2.18) – модуль напряженности электрического поля точечного тела с электрическим зарядом q1 в т.А. В соответствии с формулами (2.16), (2.17) и (2.18) поток вектора
(2.18) – модуль напряженности электрического поля точечного тела с электрическим зарядом q1 в т.А. В соответствии с формулами (2.16), (2.17) и (2.18) поток вектора 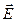 через сферическую поверхность
через сферическую поверхность
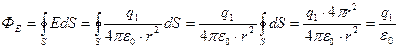 .
.
 Полученный результат
Полученный результат 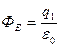 называется теоремой Гаусса: поток вектора
называется теоремой Гаусса: поток вектора 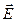 через сферическую поверхность, внутри которой в ее центре находится точечное тело с электрическим зарядом q1, равен отношению этого электрического заряда к электрической постоянной
через сферическую поверхность, внутри которой в ее центре находится точечное тело с электрическим зарядом q1, равен отношению этого электрического заряда к электрической постоянной 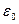 . Точнее, это теорема Гаусса в простейшем частном случае.
. Точнее, это теорема Гаусса в простейшем частном случае.
Докажите самостоятельно, что 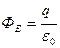 и в тех случаях, когда точечное тело с электрическим зарядом q находится внутри сферической поверхности, но не в ее центре, либо когда точечное тело с электрическим зарядом q находится внутри замкнутой поверхности произвольной формы.
и в тех случаях, когда точечное тело с электрическим зарядом q находится внутри сферической поверхности, но не в ее центре, либо когда точечное тело с электрическим зарядом q находится внутри замкнутой поверхности произвольной формы.
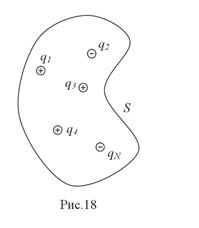 Рассмотрим общий случай, когда в объеме V, ограниченном замкнутой поверхностью, находится N точечных тел с электрическими зарядами (рис.18). (Будем считать, что в двух предыдущих частных случаях теорема Гаусса доказана.) В соответствии с принципом суперпозиции для любой точки замкнутой поверхности
Рассмотрим общий случай, когда в объеме V, ограниченном замкнутой поверхностью, находится N точечных тел с электрическими зарядами (рис.18). (Будем считать, что в двух предыдущих частных случаях теорема Гаусса доказана.) В соответствии с принципом суперпозиции для любой точки замкнутой поверхности 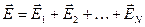 и
и 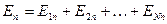 (2.19). Подставим (2.19) в определение (2.16):
(2.19). Подставим (2.19) в определение (2.16): 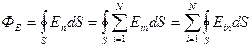 (2.20)
(2.20) 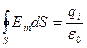 (2.21) при любой замкнутой поверхности и при любом расположении точечного тела с электрическим зарядом qi внутри этой поверхности. Из (2.20) И (2.21) получаем
(2.21) при любой замкнутой поверхности и при любом расположении точечного тела с электрическим зарядом qi внутри этой поверхности. Из (2.20) И (2.21) получаем 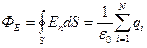 (2.22). Формула (2.22) является математической записью теоремы Гаусса в общем случае: поток напряженности электрического поля через любую замкнутую поверхность равен отношению алгебраической суммы электрических зарядов точечных тел, находящихся в объеме, ограниченном этой поверхностью, к электрической постоянной
(2.22). Формула (2.22) является математической записью теоремы Гаусса в общем случае: поток напряженности электрического поля через любую замкнутую поверхность равен отношению алгебраической суммы электрических зарядов точечных тел, находящихся в объеме, ограниченном этой поверхностью, к электрической постоянной 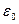 .
.
Непрерывное распределение электрического заряда по объему характеризуется плотностью электрического заряда 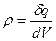 (2.23). В этом определении
(2.23). В этом определении
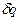 - электрический заряд в малом объеме dV,
- электрический заряд в малом объеме dV, 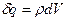 .
.
Если плотность электрического заряда задана как функция координат 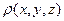 во всем объеме V, то электрический заряд в этом объеме
во всем объеме V, то электрический заряд в этом объеме 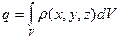 (2.24). В этом случае сумму в (2.22) нужно заменить интегралом (2.24):
(2.24). В этом случае сумму в (2.22) нужно заменить интегралом (2.24): 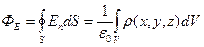 (2.25). Равенство (2.25) является математической записью теоремы Гаусса в случае непрерывного распределения электрического заряда по объему V, ограниченному замкнутой поверхностью площадью S.
(2.25). Равенство (2.25) является математической записью теоремы Гаусса в случае непрерывного распределения электрического заряда по объему V, ограниченному замкнутой поверхностью площадью S.

|
|
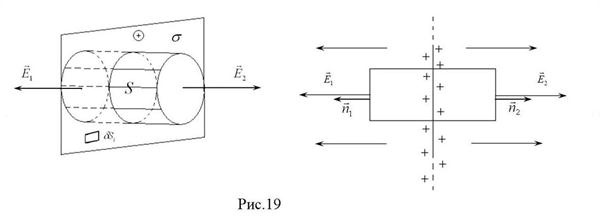
 4. Примеры применения теоремы Гаусса. Рассмотрим электрическое поле бесконечно протяженной плоскости с постоянной поверхностной плотностью электрического заряда
4. Примеры применения теоремы Гаусса. Рассмотрим электрическое поле бесконечно протяженной плоскости с постоянной поверхностной плотностью электрического заряда 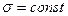 (рис.19).
(рис.19).
 Из определения (2.13)
Из определения (2.13) 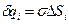 . Вычислим электрический заряд на поверхности с площадью S:
. Вычислим электрический заряд на поверхности с площадью S: 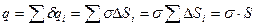 (2.26). Заключим часть плоскости с площадью S внутрь цилиндра, образующая которого перпендикулярна плоскости, а его основания имеют площадь S. В этом случае поток вектора
(2.26). Заключим часть плоскости с площадью S внутрь цилиндра, образующая которого перпендикулярна плоскости, а его основания имеют площадь S. В этом случае поток вектора 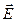 через боковую поверхность равен нулю, значит, поток вектора
через боковую поверхность равен нулю, значит, поток вектора 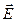 через всю поверхность цилиндра – это поток напряженности электрического поля через его основания:
через всю поверхность цилиндра – это поток напряженности электрического поля через его основания: 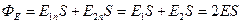 (2.27). По теореме Гаусса с учетом (2.26) получаем
(2.27). По теореме Гаусса с учетом (2.26) получаем 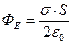 (2.28). Приравнивая правые части (2.27) и (2.28), получаем
(2.28). Приравнивая правые части (2.27) и (2.28), получаем 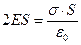 , отсюда
, отсюда 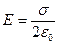 (2.29) – формула для вычисления модуля напряженности электрического поля в точках по обе стороны от плоскости с постоянной поверхностной плотностью электрического заряда. Если электрический заряд плоскости отрицательный, то формулу (2.29) надо записать в виде
(2.29) – формула для вычисления модуля напряженности электрического поля в точках по обе стороны от плоскости с постоянной поверхностной плотностью электрического заряда. Если электрический заряд плоскости отрицательный, то формулу (2.29) надо записать в виде 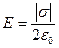 .
.
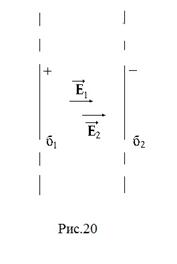
Рассмотрим электрическое поле между двумя параллельными бесконечно протяженными плоскостями с электрическими зарядами противоположных знаков при условии 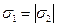 (рис.20). В этом случае
(рис.20). В этом случае 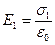 ,
, 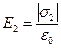 , то есть
, то есть 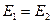 . По принципу суперпозиции в любой точке между плоскостями
. По принципу суперпозиции в любой точке между плоскостями 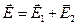 . Так как
. Так как 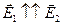 и
и 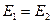 , то
, то 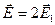 ,
, 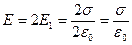 .
.
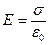 (2.30) – формула для вычисления модуля напряженности электрического поля в точках между двумя параллельными плоскостями с электрическими зарядами противоположных знаков и равными модулями поверхностных плотностей электрических зарядов.
(2.30) – формула для вычисления модуля напряженности электрического поля в точках между двумя параллельными плоскостями с электрическими зарядами противоположных знаков и равными модулями поверхностных плотностей электрических зарядов.
Получите самостоятельно формулы для модуля напряженности электрического поля бесконечно длинной цилиндрической поверхности с постоянной поверхностной плотностью электрического заряда и электрического поля сферической поверхности с электрическим зарядом q.
| <== предыдущая страница | | | следующая страница ==> |
| | | КИНЕТИКА |
Дата добавления: 2014-03-11; просмотров: 1477; Нарушение авторских прав

Мы поможем в написании ваших работ!