
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
МЕТОД НАЛОЖЕНИЯ (ТЕОРЕМА СУПЕРПОЗИЦИИ)
Все линейные цепи обладают важным свойством, позволяющим упростить анализ таких цепей, а именно: отклик линейной цепи ни сумму многих воздействий равен сумме откликов на каждое воздействие по отдельности. По сути, это есть формулировка фундаментального положения теории цепей, называемого методом наложения (суперпозиции)
Принцип суперпозиции вытекает из теории линейных дифференциальных уравнений с постоянными коэффициентами. Именно к таким уравнениям сводятся задачи анализа процессов в линейных цепях. Предположим, что требуется вычислить функцию s(t) (это может быть ток или напряжение), представляющую собой реакцию линейной цепи на внешнее воздействие f(t). Для линейной цепи функция s(t) удовлетворяет линейному дифференциальному уравнению с постоянными коэффициентами (3.1). Пусть внешнее воздействие – функция f(t) из правой части уравнения (3.1) – представляет собой сумму двух функций: f(t) = f1(t) + f2(t). В теории линейных дифференциальных уравнений с постоянными коэффициентами утверждается, что, когда справа стоит f1(t) или f2(t), допустимо решать уравнение (3.1) порознь для разных правых частей. Пусть в первом случае решением будет s1(t), а во втором: s2(t). Тогда сумма двух решений – s(t) = = s1(t) + s2(t) – окажется решением исходного уравнения с правой частью f(t), представимой в виде: f(t) = f1(t) + f2(t).
Очевидное свойство линейных дифференциальных уравнений с постоянными коэффициентами: умножение f(t) на постоянное число А влечет умножение решения s(t) на то же число А.
При использований принципа суперпозиции разбиение сложного сигнала на простейшие сводится к мысленной замене единого источника сложной по форме ЭДС на совокупность последовательно соединенных источников ЭДС, вырабатывающих тестовые сигналы. Это могут быть, например, источники гармонических напряжений разной амплитуды, частоты и начальной фазы или источники ступеней напряжения определенной высоты, возникающих в определенные моменты времени. Таких источников может быть сколь угодно много (при мысленном представлении). Идеальный источник тока сложной формы при аналогичном подходе заменяют совокупностью параллельно соединенных источников тока. Эти источники генерируют токи простейшей формы, характеризуемые определенными параметрами, например высотой ступени и моментом времени скачка тока.
Выделение единственного источника простейшего сигнала из многих, формирующих в совокупности сложный исходный сигнал, сводится к исключению прочих источников. Исключение источников выполняют следующим образом: источники ЭДС заменяют идеальными проводниками, источники тока – разрывами цепи.
Сказанное выше о замене многих источников на единственный и исключении остальных касается независимых источников тока и напряжения. Если в цепи присутствуют зависимые источники тока или напряжения (линейные элементы), то при всех преобразованиях, производимых мысленно над цепью, эти источники сохраняются в составе цепи.
Таким образом, в тех случаях, когда в линейной ЭЦ действует два или более источника электрической энергии, результирующая реакция (ток и напряжение) может быть получена как сумма отдельных реакций (наложение) от поочередного действия каждого отдельно взятого источника, в то время как действия других источников равны нулю, а они сами заменены их внутренними сопротивлениями. Источник ЭДС, который мы считаем равным нулю, означает En = 0, что эквивалентно замене его закороченной ветвью. Источник тока, который мы считаем равным нулю, означает Jn = 0, что эквивалентно замещению источника тока разомкнутой ветвью.
ПРАВИЛО ЗНАКОВ. Реакции цепи, совпадающие по направлению с результирующей реакцией, берутся со знаком плюс, в противном случае – со знаком минус.
Метод наложения применяется для обоснования других методов анализа, в частности метода компенсации и когда в схеме с несколькими источниками изменяются параметры одного из них.
Пример. В ЭЦ (рис. 4.1) рассчитать напряжение U0 методом наложения.
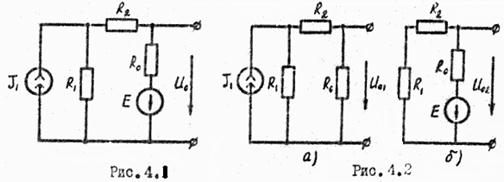
Разобьем решение задачи на три этапа: расчет ЭЦ от каждого источника в отдельности (два этапа) и наложение решений (третий этап).
Из рис. 4.2а по правилу деления токов (примечание 1) получаем реакцию цепи U01 на действие только источника тока J1:
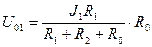
Из (рис. 4.2б) по правилу деления напряжения (примечание 2) получаем реакцию цепи U02 на действие только источника ЭДС Е:
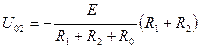
Далее, используя метод наложения, получим результирующую реакцию (искомое U0), как сумму отдельных реакций:
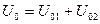
Если в рассматриваемой схеме один из источников, например Е, будет принимать различные значения и при этом требуется определить изменения U0, то для этого достаточно рассчитать U02 при заданных Е и воспользоваться последним выражением, где U01 всегда будет постоянной величиной.
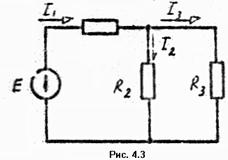 Примечание 1. Правило деления токов. По этому правилу можно определить токи, протекающие через параллельно включенные резисторы R2 и R3 (рис. 4.3), если известен входной ток I1 или известно значение ЭДС Е:
Примечание 1. Правило деления токов. По этому правилу можно определить токи, протекающие через параллельно включенные резисторы R2 и R3 (рис. 4.3), если известен входной ток I1 или известно значение ЭДС Е:
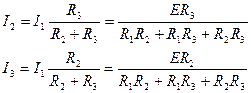
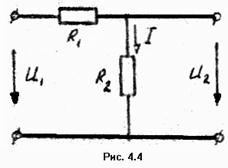
Примечание 2. Правило деления напряжения. По этому правилу можно рассчитать выходное напряжение U2 (рис. 4.4), если известны входное напряжение U1 и сопротивления двух последовательно соединенных резисторов R1 и R2.
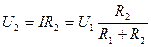
| <== предыдущая страница | | | следующая страница ==> |
| ПРАВИЛО ЗНАКОВ | | |
Дата добавления: 2014-07-19; просмотров: 814; Нарушение авторских прав

Мы поможем в написании ваших работ!