ДУ 1-го порядка. Теорема о существовании и единственности решения

Рассмотрим уравнение вида

(4)

где: - функция 2-х переменных.

Обозначим Г- множество точек на плоскости О_xy, на котором определена. Это множество является открытым, т.е. вместе с каждой своей точкой оно содержит и некоторую окрестность этой точки. В каждой точке Г задан угол наклона касательной к функции y(x), поскольку в левой части (4) стоит производная 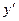, а в правой – функция .

Решение уравнения (4) означает нахождение семейства кривых, отвечающих заданному полю направлений.

Теорема Пусть в ДУ(4) функция и её частная производная непрерывна на множестве Г. Тогда:

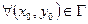
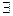
1. 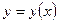- решение (4), удовлетворяющее условию

2. Если два решения y=y₁(x) и y=y₂(x) уравнения (4) совпадают хотя бы для одного значения x=x₀, то эти решения совпадают и для всех значений х, для которых они определены.

Геометрический смысл теоремы: через каждую точку Г проходит одна и только одна интегральная кривая уравнения (4).

Дата добавления: 2014-02-28; просмотров: 723; Нарушение авторских прав

Мы поможем в написании ваших работ!