
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выбор исходного допустимого базисного решения
Пусть задача ЛП задана в стандартной форме,где ограничения имеют вид неравенств:
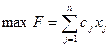
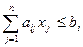 (
(  );
); 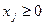 (
( 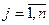 ).
).
Для перехода к канонической форме вводятся неотрицательные слабые переменные 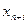 (
(  ), и ограничения принимают вид:
), и ограничения принимают вид:
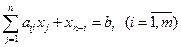 ,
, 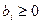
Тогда в качестве исходных базисных переменныхвыбираются 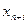 (
(  ), число которых совпадает с числом уравнений m. При
), число которых совпадает с числом уравнений m. При 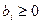 все они удовлетворяют условиям неотрицательности. Таким образом, исходное допустимое базисное решение:
все они удовлетворяют условиям неотрицательности. Таким образом, исходное допустимое базисное решение:
 (
( 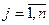 );
); 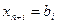 (
(  )
)
Если задача ЛП задана в канонической форме,то для получения исходного допустимого базисного решения используются специальные методы.
Пусть задача ЛП представлена в виде:
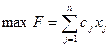 (n>m)
(n>m)
при ограничениях:
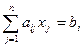 (
(  );
); 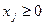 (
( 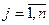 ),
), 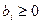 (
(  ).
).
| <== предыдущая страница | | | следующая страница ==> |
| Табличная форма симплекс – метода | | | Метод минимизации невязок |
Дата добавления: 2014-08-04; просмотров: 419; Нарушение авторских прав

Мы поможем в написании ваших работ!