Метод минимизации невязок

Рассматривается следующая вспомогательная задача:

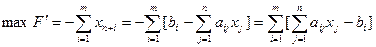
при ограничениях:

( ) ;

( )

( ).

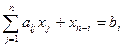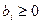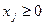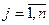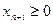Эта задача получена путем введения искусственных переменных (невязок) 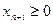( ) с требованием минимизации их суммы.

Для решения этой задачи можно использовать симплекс – метод, т. к. исходное допустимое базисное решение имеется:

( )

( ).

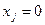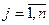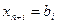Значение целевой функции 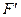не может превышать нулевой величины. Поэтому возможны два итога:

1) В результате решения вспомогательной задачи ЛП получено оптимальное значение 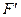=0. Соответствующее допустимое базисное решение имеет вид:

( ) ( ).

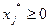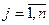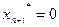Так как все искусственные переменные равны нулю, то решение вспомогательной задачи удовлетворяет условиям исходной задачи. Поэтому вектор 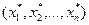является допустимым базисным решением исходной задачи.

2) В случае 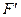<0 исходная задача не имеет ни одного допустимого базисного решения, т. е. является неразрешимой.

Действительно, если хотя бы одно такое решение существовало, то оно должно было бы совпадать с допустимым решением вспомогательной задачи при дополнительных условиях 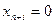, т. к. в постановке присутствует требование 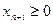при минимизации их суммы.

Таким образом, при использовании метода минимизации невязок решение задачи ЛП разбивается на два этапа. На первом этапе решается вспомогательная задача для определения исходного допустимого базисного решения, на втором определяется оптимальное решение исходной задачи ЛП.

Примериспользования метода минимизации невязок.

Пусть требуется решить следующую задачу ЛП:

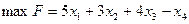
при ограничениях:

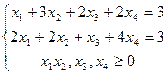
Составим вспомогательную задачу вида:

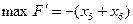
при ограничениях:

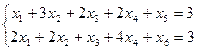
Представим целевую функцию 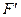через другие переменные:

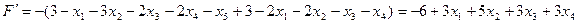
Для записи в симплекс таблицу перепишем это выражение как

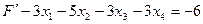
Симплекс – таблица:

Номер итерации	F, 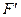и базовая переменная	Значения
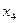
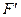
		-6	-3	-5	-3	-3
			3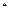
F		-5	-3	-4
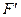
		-1	-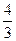
				-	-	-
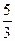
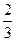
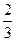
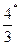
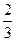
F		-4		-2
							-
				-	-	-
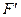
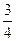
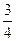
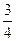
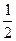
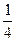
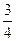
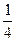
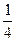
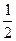
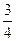
F				-3		-1

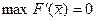в точке ( ):

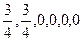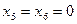
Следовательно, ( 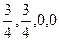) и должно быть решением исходной задачи, в этой точке 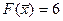, причем 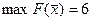не достигнут.

Далее решается исходная задача по таблице.

Дата добавления: 2014-08-04; просмотров: 951; Нарушение авторских прав

Мы поможем в написании ваших работ!