
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Неполные ДУ 1-го порядка и уравнения с разрешающимися переменными
Уравнение (4) называется неполным, если функция  явно зависит либо только от х, либо только от y. Здесь возможны два случая.
явно зависит либо только от х, либо только от y. Здесь возможны два случая.
1. Уравнение 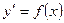 или
или 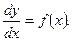 Переменная его в виде
Переменная его в виде 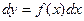 , откуда его решение
, откуда его решение 
2. Уравнение  удобно решать в виде
удобно решать в виде 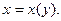 Перепишем в виде
Перепишем в виде  , и его решение будет
, и его решение будет 
Уравнение (4) называется уравнением с разделяющимися переменными, если оно может быть представлено в виде:
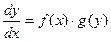
или
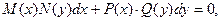
где  -функции
-функции 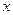 ,
, 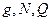 -функции
-функции 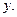
Для решения такого уравнения его следует преобразовать к виду, в котором дифференциал и функции от 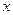 окажутся в одной части равенства, а дифференциал и функции от
окажутся в одной части равенства, а дифференциал и функции от 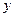 - в другой. Затем проинтегрировать обе части полученного равенства:
- в другой. Затем проинтегрировать обе части полученного равенства:
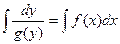 или
или 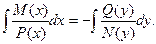
Пример. Решить уравнение
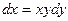 .
.
Разделим левую и правую части уравнения на  при
при  , тогда
, тогда

Интегрируем:
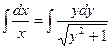
Делаем замену переменной: 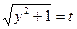 ;
; 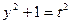 ;
; 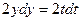 ; тогда:
; тогда:


Это решение можно переписать в виде:

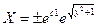 или
или 
Уравнения вида 
где a, b – числа, приводятся к уравнениям с разделяющимися переменными заменой 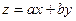 ; тогда
; тогда 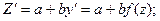


| <== предыдущая страница | | | следующая страница ==> |
| ДУ 1-го порядка. Теорема о существовании и единственности решения | | | Однородные ДУ 1-го порядка |
Дата добавления: 2014-02-28; просмотров: 698; Нарушение авторских прав

Мы поможем в написании ваших работ!