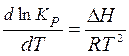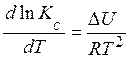Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Влияние температуры на химическое равновесие. Уравнения изобары и изохоры химической реакции
Влияние температуры на химическое равновесие определяется зависимостью константы равновесия от температуры. Запишем уравнение Гиббса—Гельмгольца (2.64):
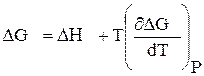(3.27)
Для смеси идеальных газов
DG = RT lnΠP 
-RT lnKP (3.28)
Возьмем производную этого выражения по температуре, считая, что численные значения начальных парциальных давлений заданы, так что ΠP =const:
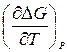= RlnΠP -RlnKP-RT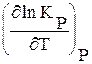 
(3.29)
Так как общее давление по условию постоянно, можно перейти к значкам полного дифференциала. Подставляя два последних выражения в (3.27), получим:
|
(3.30)
Уравнение (3.30) называется уравнением изобары химической реакции Вант-Гоффа (в дифференциальной форме).
Аналогично можно получить для изохорных условий:
|
(3.31)
Это уравнение называют уравнением изохоры химической реакции Вант-Гоффа.
Из уравнений (3.30) и (3.31) видно, что зависимость константы химического равновесия от температуры определяется знаком теплового эффекта реакции DH (или DU). Проанализируем уравнение (3.30):
* если DH <0 , т.е. процесс экзотермический, то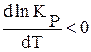 
, т.е. с ростом температуры константа равновесия КP уменьшается, равновесие химической реакции смещается влево, в направлении образования исходных веществ;
* если DH >0 , т.е. процесс эндотермический, то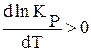 
, т.е. с ростом температуры константа равновесия КP увеличивается, равновесие химической реакции смещается вправо, в направлении образования продуктов реакции;
* если DH = 0 , то КPне зависит от температуры.
Аналогично - для уравнения изохоры.
Эти выводы соответствуют принципу смещения равновесия Ле Шателье - Брауна.
Решение уравнений изобары и изохоры химических реакций позволяет находить константы равновесия при различных температурах. Покажем это на примере уравнения изобары.
Проинтегрируем уравнение (3.30), представив его в виде:
(3.32)
Если интервал Т1 ¸Т2 не велик, то можно считать, что DН постоянно. Тогда интегрирование (3.32) в пределах от КP,Т1 до КP,Т2 и от Т1 до Т2 дает:
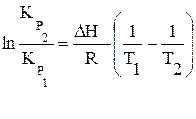(3.33)
| <== предыдущая страница | | | следующая страница ==> |
| Уравнение изотермы и направление химической реакции. Принцип смещения равновесия Ле Шателье - Брауна | | | Уравнение (3.33) является уравнением изобары химической реакции в интегральной форме |
Дата добавления: 2014-10-02; просмотров: 780; Нарушение авторских прав
Мы поможем в написании ваших работ!