
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
ДУ 2-го порядка, допускающие понижение порядка
Если ДУ имеет вид 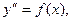 то оно решается последовательным интегрированием.
то оно решается последовательным интегрированием.
Если в запись уравнения не входит искомая функция, то такое уравнение
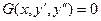
можно решить, найдя сначала вспомогательную функцию 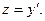
Если в уравнение не входит 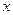 , то оно имеет вид –
, то оно имеет вид –
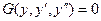 .
.
В этом случае порядок уравнения можно понизить, если за независимую переменную взять 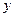 , а за неизвестную функцию
, а за неизвестную функцию  Тогда
Тогда
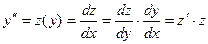
Пример. 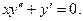
Положим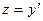 , тогда
, тогда  , уравнение принимает вид:
, уравнение принимает вид:

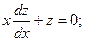
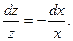
 Интегрируя, получаем:
Интегрируя, получаем:  или
или 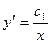 ;
; 

Пример. 
Положим 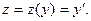 Тогда
Тогда 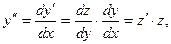
уравнение принимает вид: 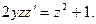 Это уравнение с разделяющимися переменными:
Это уравнение с разделяющимися переменными:

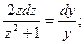
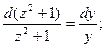
 пусть
пусть  , тогда
, тогда 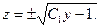


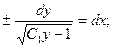
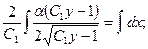
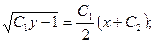

| <== предыдущая страница | | | следующая страница ==> |
| Линейные ДУ 1-го порядка | | | Линейные ДУ 2-го порядка с постоянными коэффициентами |
Дата добавления: 2014-02-28; просмотров: 634; Нарушение авторских прав

Мы поможем в написании ваших работ!