Линейные ДУ 1-го порядка

Они имеют вид

(8)

где 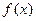, 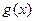- непрерывные функции. Если 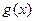=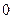, то уравнение (8) называется однородным, в противном случае – неоднородным.

Будем искать решение (8) в виде Перепишем (8) в виде:

, или

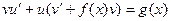
Найдём какое-либо частное решение уравнения

(9)

Тогда функция - решение уравнения

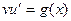(10)

Поэтому решение (8) сводится к решению двух уравнений (9) и (10) с разделяющимися переменными.

Пример. xy^'-2y=2x⁴.

Разделим уравнение на х: примем , тогда

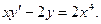
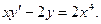
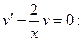
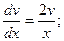
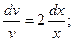
Решим уравнение или Поскольку ищем какое-либо частное решение, константой интегрирования пренебрегаем.

Далее решим уравнение или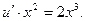

Отсюда 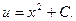Окончательно решение исходного уравнения:

Дата добавления: 2014-02-28; просмотров: 588; Нарушение авторских прав

Мы поможем в написании ваших работ!