
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Линейные дифференциальные уравнения второго порядка
Рис. 2.1
Исследуем теперь неоднородное уравнение(3.1). Будем искать решение (3.1) в виде:
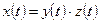 , (3.4)
, (3.4)
где 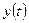 ,
,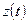 неизвестные дифференцируемые функции.
неизвестные дифференцируемые функции.
Учитывая, что 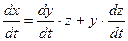 из уравнения (3.1) получим:
из уравнения (3.1) получим:
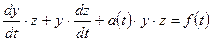 .
.
Или
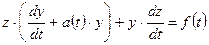 . (3.5)
. (3.5)
Будем считать, что  , то есть
, то есть 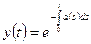 .
.
С учетом этого, уравнение (3.5) примет вид:
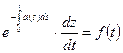 . Или
. Или 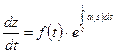 .
.
Интегрируя это уравнение, получим:
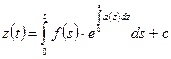 ,
,
где с - произвольная постоянная.
Таким образом, общее решение уравнения (3.1) имеет вид:
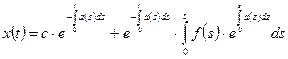 . (3.6)
. (3.6)
Определение 3. Функция 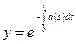 называется интегрирующим множителем для уравнения (3.1)
называется интегрирующим множителем для уравнения (3.1)
Пример 6. Внутривенное питание глюкозой.
Рассмотрим лечебную процедуру состоящую в вливании глюкозы в кровеносную систему. Пусть 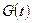 - количество глюкозы в крови пациента в момент времени
- количество глюкозы в крови пациента в момент времени 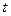 . Допустим, что глюкоза вводится в кровь с постоянной скоростью с (г/мин.). В то же время глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Таким образом, функция
. Допустим, что глюкоза вводится в кровь с постоянной скоростью с (г/мин.). В то же время глюкоза разлагается и удаляется из кровеносной системы со скоростью, пропорциональной имеющемуся количеству глюкозы. Таким образом, функция 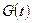 удовлетворяет дифференциальному уравнению первого порядка
удовлетворяет дифференциальному уравнению первого порядка
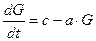 , (3.7)
, (3.7)
где 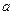 - положительная постоянная. Это неоднородное линейное дифференциальное уравнение первого порядка вида (3.1) при
- положительная постоянная. Это неоднородное линейное дифференциальное уравнение первого порядка вида (3.1) при 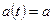 и
и 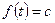 .
.
Чтобы решить это уравнение, запишем его в виде: 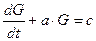 .
.
Умножив последнее уравнение на интегрирующий множитель 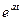 , и учитывая, что
, и учитывая, что
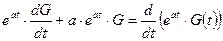
получим:
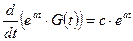 .
.
Интегрируя, получаем:
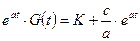 ,
,
где 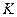 - постоянная интегрирования.
- постоянная интегрирования.
Таким образом, общее решение (3.7) имеет вид:
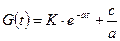 . (3.8)
. (3.8)
Если известна начальная концентрация глюкозы в крови 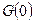 , то из (3.8)имеем:
, то из (3.8)имеем:
 .
.
Значит, общее решение может быть записано в виде:
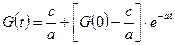 . (3.9)
. (3.9)
Из (3.9) следует, что с увеличением времени 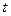 содержание глюкозы в крови
содержание глюкозы в крови 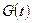 приближается к числу
приближается к числу 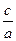 , которое есть равновесное количество глюкозы в крови.
, которое есть равновесное количество глюкозы в крови.
Пример 7. В популяцию людей большой численности занесено инфекционное заболевание. Доля людей, перенесших заболевание, возрастает со временем. Пусть 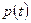 обозначает долю людей, переболевших этой болезнью за
обозначает долю людей, переболевших этой болезнью за 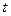 лет после ее возникновения в популяции, и пусть
лет после ее возникновения в популяции, и пусть
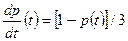 .
.
Найдите 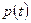
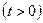 , если
, если 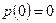 . За сколько лет доля переболевших достигнет
. За сколько лет доля переболевших достигнет  ?
?
Решение:Запишем уравнение в виде:
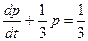 .
.
Умножив на 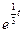 и учитывая, что
и учитывая, что
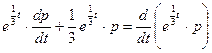
получим:
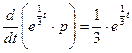 .
.
Интегрируя, находим:
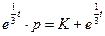 . или
. или 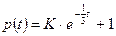 .
.
Учитывая, что 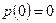 имеем:
имеем:  .
.
Таким образом 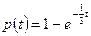 .
.
Пусть 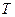 - время, при котором доля переболевших людей достигнет
- время, при котором доля переболевших людей достигнет  , т.е.
, т.е.
 .
.
Отсюда находим:
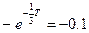 ;
; 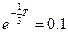 ;
; 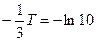 ;
; 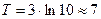 .
.
Таким образом, доля переболевших людей достигнет  через 7 лет.
через 7 лет.
2.2. Нелинейные дифференциальные уравнения первого порядка:
метод разделения переменных
Общий вид нелинейного уравнения следующий:
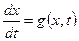 , (3.10)
, (3.10)
где 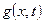 - заданная непрерывная функция.
- заданная непрерывная функция.
Биологическая интерпретация уравнения (3.10) заключается в том, что скорость роста популяции является функцией времени и размера популяции. В общем случае не удается отыскать формулу, дающую в явном виде решение уравнения(3.10). Однако имеются некоторые специальные типы нелинейных уравнений первого порядка, решение которых можно найти в явном виде. Одним из таких уравнений является уравнение с разделяющимися переменными.
Будем говорить, что переменные 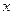 и
и 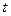 в уравнении (3.10) разделяются, если:
в уравнении (3.10) разделяются, если:
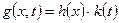 ,
,
где 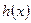 - представляет собой функцию только от
- представляет собой функцию только от 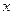 , а
, а 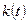 - функцию только от
- функцию только от 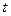 . В этом случае уравнение (3.10) записывается в виде:
. В этом случае уравнение (3.10) записывается в виде:
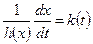 . или
. или  . (3.11)
. (3.11)
В такой форме левая часть интегрируется по переменной 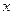 , а правая часть интегрируется по переменной
, а правая часть интегрируется по переменной 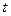 . Выполняя эти два интегрирования, приходим к общему решению
. Выполняя эти два интегрирования, приходим к общему решению
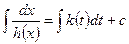 . (3.12)
. (3.12)
Если 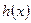 и
и 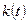 достаточно простые, то можно найти эти интегралы и получить общее решение
достаточно простые, то можно найти эти интегралы и получить общее решение 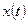 в явном виде.
в явном виде.
Пример 8. Логистический закон развития.
Скорость роста популяции в расчете на одну особь представляет собой разность между средней рождаемостью и средней смертностью. Будем считать, что средняя рождаемость выражается положительной постоянной 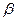 , не зависящей от времени
, не зависящей от времени 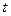 и размера популяции
и размера популяции 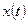 . Допустим также, что средняя смертность пропорциональна размеру популяции и поэтому равна
. Допустим также, что средняя смертность пропорциональна размеру популяции и поэтому равна 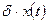 , где
, где 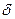 - положительная постоянная. Это увеличение смертности с ростом популяции может происходить за счет конкуренции за доступные пищевые ресурсы.
- положительная постоянная. Это увеличение смертности с ростом популяции может происходить за счет конкуренции за доступные пищевые ресурсы.
В данном случае, популяция подчиняется уравнению 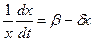 .
.
Или
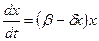 . (3.13)
. (3.13)
Разделяя переменные, получим:
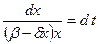 .
.
Интегрируя, имеем:
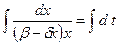 .
.
Учитывая, что
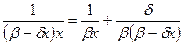
имеем:
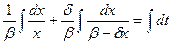 ;
; 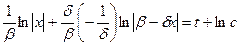 ;
;
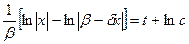 ;
; 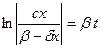 ;
; 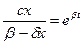 .
.
Разрешая последнее уравнение относительно 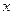 , находим:
, находим:
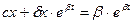 ;
;
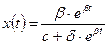 . (3.14)
. (3.14)
Если 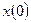 есть размер начальной популяции, то
есть размер начальной популяции, то
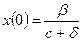 ;
; 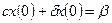 ;
;  .
.
Подставив последнее в(3.14), получим:
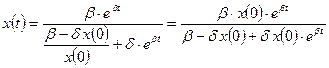 . (3.15)
. (3.15)
Процесс роста, описываемый функцией (2.15) называется логистическим ростом, а уравнение (2.13)- логистическим уравнением.
При логистическом росте популяции с увеличением времени популяция приближается к предельному (равновесному) размеру, равному 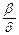 . То есть размер равновесной популяции прямо пропорционален средней рождаемости и обратно пропорционально средней смертности на одну особь.
. То есть размер равновесной популяции прямо пропорционален средней рождаемости и обратно пропорционально средней смертности на одну особь.
Определение 4. Линейным дифференциальным уравнением второго порядка называется уравнение вида:
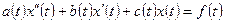 , (3.16)
, (3.16)
где 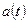 ,
, 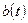 ,
, 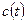 и
и 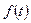 - заданные функции, причем
- заданные функции, причем 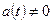 . Здесь, для удобства записи использованы обозначения
. Здесь, для удобства записи использованы обозначения 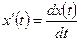 ,
, 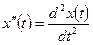 .
.
Если функции 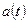 ,
,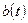 ,
,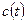 постоянны, то уравнение (3.16) называют уравнением с постоянными коэффициентами.
постоянны, то уравнение (3.16) называют уравнением с постоянными коэффициентами.
Если 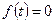 при всех значениях
при всех значениях 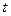 , то уравнение называют однородным.
, то уравнение называют однородным.
Рассмотрим однородное уравнение с постоянными коэффициентами:
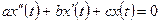 , (3.17)
, (3.17)
где 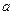 ,
,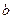 ,
,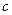 - постоянные, причем
- постоянные, причем 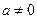 .
.
Решение уравнения (3.17) будем искать в виде:
 ,
,
где 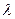 - некоторое число.
- некоторое число.
Учитывая, что 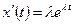 ,
, 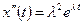 из (3.17) имеем:
из (3.17) имеем:
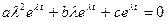 .
.
Или
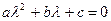 . (3.18)
. (3.18)
Уравнение (3.18) называется характеристическим уравнением для уравнения(3.17). Корнями характеристического уравнения служат
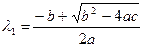 ,
, 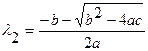 . (3.19)
. (3.19)
Нужно рассмотреть три случая: величина  больше нуля, равна нулю или меньше нуля.
больше нуля, равна нулю или меньше нуля.
Случай 1. Пусть 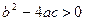 , т.е.
, т.е. 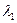 и
и  действительны и различны. Тогда дифференциальное уравнение имеет два разных решения:
действительны и различны. Тогда дифференциальное уравнение имеет два разных решения: и
и 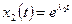 . Общее решение записывается в виде:
. Общее решение записывается в виде:
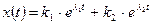 , (3.20)
, (3.20)
где 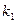 и
и 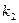 - произвольные постоянные. Чтобы найти
- произвольные постоянные. Чтобы найти 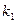 и
и 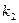 нужно знать два условия, которым должно удовлетворять решение
нужно знать два условия, которым должно удовлетворять решение 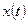 , например,
, например, 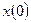 и
и  .
.
Случай 2. Пусть  . В этом случае корни характеристического уравнения равны между собой:
. В этом случае корни характеристического уравнения равны между собой: 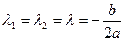 . Одним решением (3.17) является функция
. Одним решением (3.17) является функция 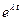 , а другим
, а другим 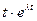 . Общее решение имеет вид:
. Общее решение имеет вид:
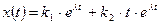 . (3.21)
. (3.21)
Случай 3. Пусть  . В этом случае корни характеристического уравнения (3.18) представляют собой комплексно-сопряженные числа
. В этом случае корни характеристического уравнения (3.18) представляют собой комплексно-сопряженные числа
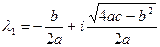 и
и 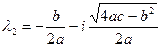 .
.
Общее решение уравнения (3.17 запишется в виде:
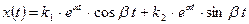 , (3.22)
, (3.22)
где 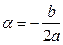 ,
,  .
.
Пример 9. В благоприятных условиях выращивают две популяции мух. Для популяции I удельная скорость роста составляет 0.1, если время выражается в днях. Для популяции II аналогичная скорость составляет 0.08. Определим 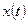 как суммарную численность двух популяций в момент
как суммарную численность двух популяций в момент 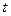 . Найти дифференциальное уравнение второго порядка, которому удовлетворяет
. Найти дифференциальное уравнение второго порядка, которому удовлетворяет 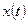 .
.
Решение: По условию задачи 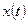 - суммарная численность двух популяций мух. Учитывая, что
- суммарная численность двух популяций мух. Учитывая, что 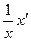 - есть удельная скорость роста, то для
- есть удельная скорость роста, то для 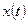 имеем уравнение
имеем уравнение
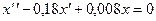 .
.
Это есть дифференциальное уравнение второго порядка, которому удовлетворяет 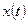 . Решая, находим:
. Решая, находим:
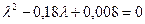 .
.
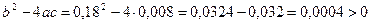 .
.
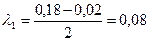 ;
; 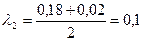 .
.
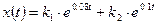 - общее решение уравнения.
- общее решение уравнения.
| <== предыдущая страница | | | следующая страница ==> |
| Линейные дифференциальные уравнения первого порядка | | | Упражнения |
Дата добавления: 2014-03-11; просмотров: 817; Нарушение авторских прав

Мы поможем в написании ваших работ!