Дифференциальные уравнения конвективного теплообмена

В общем случае однофазная химически однородная текучая среда характеризуется:

1. полем температуры 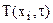– скалярное поле;

2. полем скорости 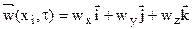– векторное поле;

3. полем давления 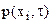– скалярное поле,

где x_i – ортогональная система координат (например, для декартовой системы координат 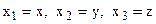); 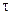– время. При этом физические свойства среды (плотность, коэффициенты вязкости, коэффициент теплопроводности) должны быть известны.

Для расчета температуры, давления и, в общем случае, трех составляющих вектора скорости необходимо решить пять дифференциальных уравнений:

— дифференциальное уравнение переноса энергии в текучей среде – уравнение Фурье-Кирхгофа;

— три дифференциальных уравнения переноса импульса в текучей среде – уравнения Навье - Стокса;

— дифференциальное уравнение неразрывности или сплошности.

Дифференциальное уравнение Фурье-Кирхгофа

В векторном виде уравнение переноса энергии в текучей среде имеет вид

,

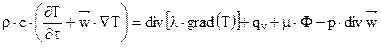где 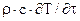– слагаемое в правой части уравнения энергии, которое отражает нестационарность процесса теплообмена; 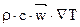– конвективный член уравнения энергии – учитывает перенос теплоты за счет движения среды; 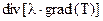– диффузионный член уравнения – учитывает перенос теплоты теплопроводностью; 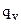– источниковый член уравнения – учитывает поступление или убыль энергии за счет действия внутренних источников или стоков теплоты; 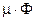– слагаемое уравнения энергии, учитывающее нагрев среды вследствие диссипации кинетической энергии движения за счет трения; 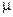– динамический коэффициент вязкости; Ф – диссипативная функция; 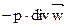– слагаемое уравнения, учитывающее изменение энергии флюида при его сжатии или расширении.

Последние два слагаемых в уравнении переноса энергии в значительной степени зависят от скорости движения и для скоростей менее 100 м/с, характерных дл энергетических и теплотехнологических агрегатов, в расчетах теплообмена не учитываются. Принимая допущение о независимости физических свойств среды от температуры и отсутствии внутренних источников теплоты уравнение Фурье-Кирхгофа принимает вид:

,

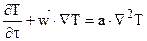где 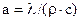– коэффициент температуропроводности текучей среды.

Заметим, что для неподвижной среды (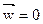) уравнение Фурье-Кирхгофа переходит в уравнение теплопроводности – уравнение Фурье.

Для решения уравнения Фурье-Кирхгофа необходимо предварительно рассчитать поле скорости, решив уравнения Навье - Стокса.

Дифференциальные уравнения движения текучей среды

(уравнения Навье - Стокса)

Вывод уравнения основан на законе сохранения количества движения: для фиксированной массы М текучей среды, согласно которому изменение импульса равно сумме внешних сил, действующих на объем массой М.

,

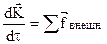где 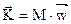- импульс; 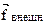– внешние силы, действующие на элементарный объем флюида.

Без вывода запишем уравнения Навье Стокса для текучих сред с постоянной плотностью в векторной форме:

.

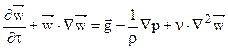В этом случае уравнение неразрывности принимает вид:

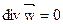
В уравнении движения текучей среды все слагаемые имеют размерность [Н/кг] и представляют собой массовую плотность силы: 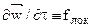– нестационарный член уравнения, имеющий смысл локальной силы; 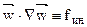– конвективный член уравнения – характеризует силу инерции; 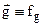– слагаемое, имеющее смысл объемной или массовой силы (силы тяжести); 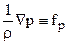– сила давления; 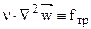– диффузионный член уравнения – характеризует силу трения.

Условия однозначности, необходимые для решения системы дифференциальных уравнений конвективного теплообмена

Для выделения единственного решения необходимо задать:

— геометрию расчетной области, ее размеры и время процесса;

— физические свойства текучей среды;

— закон изменения внутренних источников теплоты (в частном случае );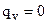

— начальные и граничные условия.

Начальные условия определяют распределение температуры, скорости, и давления в начальный момент времени процесса конвективного теплообмена во всей расчетной области

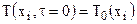
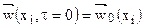
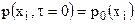
Граничные условия для уравнения энергии могут иметь вид граничных условий I, II, III и IV родов на твердых ограничивающих течение поверхностях. Например, граничные условия IV рода в этом случае имеют вид

,

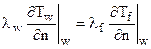где 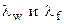– коэффициенты теплопроводности ограждений и флюида; n – нормаль к ограждающей поток поверхности.

Скорость на твердых, ограничивающих текучую среду поверхностях, равна нулю в силу условия прилипания. На свободных поверхностях расчетной области скорость должна быть, либо задана, либо рассчитана в ходе итерационного процесса.

Для расчета поля давления на твердых ограничивающих поверхностях, как правило, задают следующие граничные условия:

.

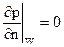Аналитическое решение системы дифференциальных уравнений конвективного теплообмена с соответствующими условиями однозначности пока не получено. В настоящее время для моделирования теплообмена в текучих средах применяют численные методы решения вышеуказанной системы дифференциальных уравнений, оформленные в виде вычислительных комплексов (пакетов прикладных программ), изучение которых далеко выходит за рамки нашего курса. Однако, не решая систему уравнений конвективного теплообмена, мы ее тем не менее будем использовать при изучении экспериментального метода расчета конвективного теплообмена, основанного на теории подобия физических процессов.

Дата добавления: 2014-03-11; просмотров: 1009; Нарушение авторских прав

Мы поможем в написании ваших работ!