Интерпретация уравнения Бернулли

Все члены уравнения Бернулли имеют линейную размерность и представляют собой напоры:

z - называется геометрическим напором (геометрической высотой), представляет собой место положения центра тяжести живого сечения элементарной струйки относи­тельно плоскости сравнения,

- называется пьезометрическим напором (пьезометрической высотой),

представляет собой высоту, на которую могла бы подняться жидкость при отсутствии движения

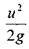- носит название скоростного напора.

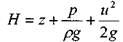- носит название гидродинамического напора

Уравнение Бернулли является выражением закона сохранения механической энер­гии движущейся жидкости, по этой причине все части уравнения представляют собой ве­личины удельной энергии жидкости:

z - удельная энергия положения,

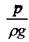- удельная энергия давления,

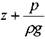- удельная потенциальная энергия,

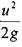- удельная кинетическая энергия

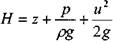- удельная механическая энергия.

Дата добавления: 2014-02-26; просмотров: 602; Нарушение авторских прав

Мы поможем в написании ваших работ!