Геометрическая интерпретация задачи ЛП

Позволяет проиллюстрировать понятие допустимого базисного решения и показать, что именно среди этих решений находится оптимальное.

Рассмотрим пример. Найти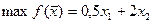

при ограничениях

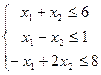
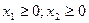
Перепишем в виде

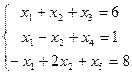
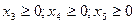
В данном примере число уравнений m = 3, а число неизвестных m + n = 5, т. е. число свободных переменных n = 2. Это дает возможность решить задачу графически в двумерном пространстве, т. е. на плоскости.

Систему трех уравнений можно решить относительно трех переменных, выразив их через остальные переменные.

В частности:

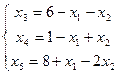
Каждое из уравнений 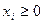, 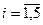определяет некоторую полуплоскость, задаваемую в координатах и .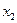

Например, 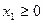определяет правую полуплоскость относительно оси 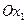, 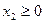- верхнюю полуплоскость относительно оси .

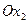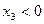
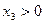
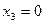
Област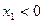и и 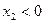считаются запрещенными и отмечаются штриховкой.

Условие 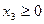определяет некоторую полуплоскость, лежащую по одну сторону от прямой 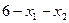, а именно ту, которая содержит начало координат.

В этом легко убедиться, если подставить координаты точки (0, 0) в уравнение 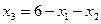и проверить значение .

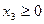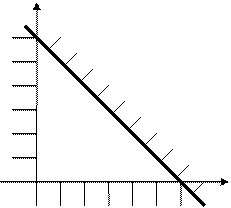
Для всех ограничений одновременно получаем

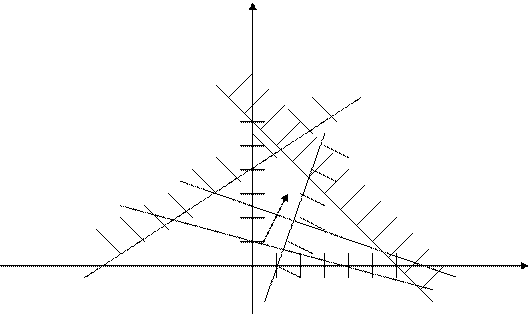
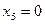
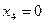
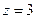
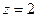
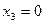
Допустимой областью значений и является выделенный многоугольник.

Чтобы получить максимум целевой функции 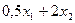рассмотрим уравнение 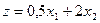, которое определяет прямую при любом фиксированном z.

Например, для z = 2 имеем 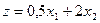(см рисунок). Увеличивая z будем получать семейство параллельных прямых. Решение оптимизационной задачи будет в той точке, где z максимально, а полученная прямая имеет хотя бы одну общую точку с допустимой областью решений.

Для обобщения результатов рассмотрим постановку задачи в виде:

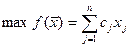(1)

семейство гиперплоскостей при ограничениях

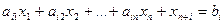( ) (2)

Уравнение (3) определяет неотрицательную область в пространстве :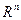

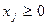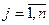( ); (3)

Полупространство, ограниченное одной из гиперплоскостей (2)

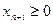( ); (4)

где имеется m уравнений в ограничениях при m + n неизвестных.

Каждое из неравенств (3) определяет в n – мерном евклидовом пространстве некоторое замкнутое полупространство. Пересечение всех этих полупространств дает неотрицательный октант (квадрант при n = 2) в n – мерном пространстве.

Пересечение всех замкнутых полупространств дает выпуклый многогранник, расположенный в неотрицательном октанте n – мерного пространства.

Примеры таких многогранников:

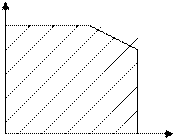
Х

n=2; m=3

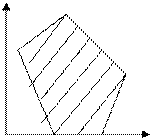
Х

n=2; m=4

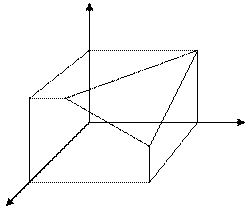
n=3; m=4

Поверхности равных значений z целевой функции представляют собой семейство параллельных гиперплоскостей (плоскостей при n = 3; прямых при n = 2). Поэтому экстремум целевойфункции в задаче ЛП достигается в одной или нескольких вершинах многогранника решений.

Замечание:Каждая вершина многогранника допустимых решений в задаче ЛП соответствует одному из допустимых базисных решений, т. к. все вершины лежат в неотрицательном октанте (все переменные неотрицательны) и для любой из них не менее n переменных равны нулю(число переменных, равных нулю, совпадает с числом пересекающихся граней).

Для поиска оптимального решения можно просмотреть все допустимые базисные решения или вершины многогранника, число которых конечно.

Однако в реальных задачах их число может быть очень большое, поэтому применяются специальные методы направленного перебора, обеспечивающие сокращение числа просматриваемых допустимых базисных решений.

Дата добавления: 2014-08-04; просмотров: 599; Нарушение авторских прав

Мы поможем в написании ваших работ!