Симплекс – метод решения задачи ЛП

Является основным методом решения задач ЛП, представленных в каноническойформе записи.

Разработан в 1949 г. американским математиком Дж. Данценгом.

Идея симплекс – метода заключается в следующем.

Сначала выбирается одно из допустимых базисных решений,соответствующее некоторой вершине многогранника.

Для этого свободные переменные приравниваются к нулю и решается система уравнений, образованная ограничениями.

Если при этомнекоторые из базисных переменных окажутся отрицательными, то необходимо выбрать другие свободные переменные, т. е. перейти к новому базису.

Далее для полученного допустимого базисного решения проверяется: достигнут ли здесь экстремум целевой функции.

Если экстремум не достигнут, то осуществляется переход к ближайшему допустимому

базисному решению, соответствующему соседней вершине многогранника, для которой

значение целевой функции возрастает (при поиске max) или убывает (при поиске min).

Рассмотрим метод на примере:

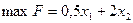
при ограничениях

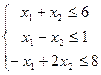
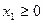
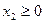
Если ввести дополнительные слабые переменные :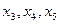

; ; ; ; .

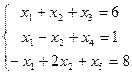
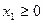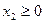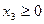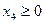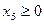Перепишем задачу в следующем виде

;

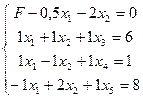
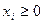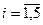
Общее число переменных m + n = 5, число уравнений в системе ограничений m = 3. Следовательно, в каждом базисном решении имеется две свободных и три базисных переменных.

Выберем в качестве свободных переменные и . Приравняем их нулю и получим базисное решение:

; ; ; ; .

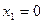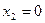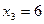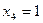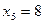Так как все переменные неотрицательны, то это решение является допустимым базисным решением, при котором значение целевой функции .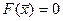

Для полученного решения максимум целевой функции F не достигнут, т. к. в выражении для целевой функции 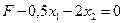обе свободные переменные и входят с отрицательным знаком. Поэтому, увеличивая значение любой из них, можно получить большее значение целевой функции F.

Но увеличивать значение свободной переменной можно только путем ее перевода вбазисные.При этом необходимо одну из базисных переменных перевести в свободные.

Укажем способ, по которому производится выбор таких переменных.

Для перевода из свободных переменных в базиснуюцелесообразно выбрать такую переменную, которая входит в выражение для целевой функции F с наибольшим по абсолютной величине отрицательным коэффициентом. В данном примере это .

При возрастании свободной переменной некоторые из базисных переменных начнут уменьшаться. Так как отрицательные значения переменных недопустимы, то в качестве новой свободной переменнойследует выбрать такую базисную переменную, которая раньше других принимает нулевое значение.

При увеличении для 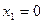уменьшаются значения переменных и . Переменная принимает нулевое значение при 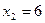; переменная 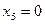при 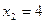. Следовательно, свободной переменной вместо должна стать переменная .

Общее правило выбора:для определения базисной переменной, переводимой в свободную, вычисляются отношения свободного члена уравнения к коэффициенту 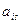при свободной переменной,переводимой в базисные. При этом отрицательные отношения не учитываются.В итоге выбирается базисная переменная, входящая в уравнение с наименьшим отношением.

В частности для второго уравнения: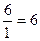

для третьего : 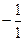- неустойчивость

для четвертого : .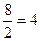

Таким образом, для перехода к новому допустимому базисному решению, увеличивающему значение F необходимо перевести:

- из свободных в базисные;

- из базисных в свободные переменные.

Все уравнения задачи необходимо переписать таким образом, чтобы в последнем уравнении (где присутствует ) коэффициент при стал равным единице, а в оставшихся строках – нулю.

Процедура, с помощью которой это достигается, называется сменой базисаи осуществляется следующим образом:

- уравнение, соответствующее базисной переменной, переводимой в свободные ( ) , делится на коэффициент при свободной переменной, переводимой в базисные ( );

- для каждого из оставшихся уравнений определяется коэффициент 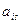при свободной переменной 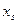, переводимой в базисные. Далее полученное на предыдущем шаге уравнение уменьшается на коэффициент (- 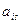) и складывается с каждым i – м уравнением.

Продолжим пример:

После первого шага, называемого нормировкой:

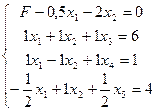
После второго шага окончательно получаем:

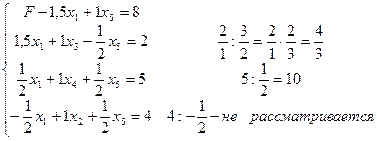
Приравняв нулю свободные переменные получим новое допустимое базисное решение и значение целевой функции:

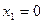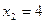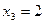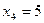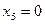; ; ; ; ;F=8.

Максимум целевой функции также не достигнут, т. к. в выражении для F переменная входит с отрицательным знаком. Поэтому следует перевести из свободных в базисные.

Чтобы определить базисную переменную, переводимую в свободные, вычисляется отношение свободных членов уравнений к коэффициентам при (справа от уравнений). Выбирается строка с минимальным положительным отношением ( 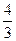). Базисная переменная из этой строки ( ) переводится в свободные.

Выполняем схему базиса и получаем:

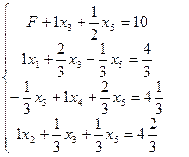
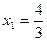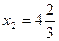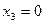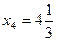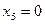; ; ; ; ;F=10.

Полученное допустимое базисное решение является решением задачи, т. к. при увеличении любой свободной переменной ( , ) значение целевой функции может только уменьшаться. Это объясняется тем, что коэффициенты при свободных переменных в выражении для F положительны.

Таким образом, в качестве критерия оптимальностиможно рассматривать знаки коэффициентов при свободных переменныхв выражении целевой функции.

В случае задачи максимизации – это неотрицательные коэффициенты в выражении целевой функции; минимизации – неположительные.

С учетом сказанного общая схема решения задачиЛП симплекс – методом имеет вид:

Начало

Выбор исходного

допустимого базиса

проверка

отличимости

решения

Нет Конец

Определение свободной переменной,

переводимой в базисные

Определение базисной переменной,

переводимой в свободные

Смена базиса

Дата добавления: 2014-08-04; просмотров: 379; Нарушение авторских прав

Мы поможем в написании ваших работ!