Базисное решение задачи ЛП

Рассмотрим стандартную задачу вида

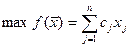
при ограничениях

( )

( ).

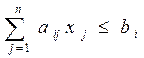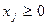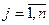Задача содержит n переменных и m ограничений, представленных в виде неравенств.

Переходя к канонической задаче получаем:

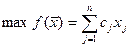(1)

при ограничениях

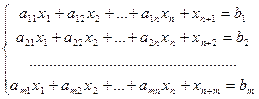(2)

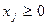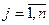( ); (3)

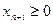( ) – слабая переменная. (4)

Система (2) имеет бесчисленное множество решений, т. к. содержит m уравнений n + m неизвестных.

Чтобы получить некоторое решение системы (2) приравниваем нулю n неизвестных. Полученная система из m уравнений с m неизвестными будет иметь решение, если определитель этой системы отличен от нуля.В противном случае можно выбрать другие n неизвестных и приравнять их к нулю.

Таким образом, базисомназывают любой набор из m переменных, для которых определитель, составленный из коэффициентов при этих переменных, не равен нулю.

Полученное при этом решение называют базисным,а переменные, которые были приравнены к нулю называются свободными.

Эти m переменных называют базисными.Остальные n переменных называютсвободными. (Свободные переменные = 0)

Т. о., если приравнять все свободные переменные нулю, то можно решить полученную систему из m уравнений с m неизвестными. Полученное при этом решение называют базисным.

Замечание:Для каждой конкретной системы (2) может существовать несколько различных базисов с различными базисными переменными и базисными решениями.

Среди возможных базисных решений могут быть такие, которые дают отрицательные значения некоторых переменных. Это противоречит постановке задачи (3), (4), а решение является недопустимым.

Допустимым базисным решением (дбр)является такое базисное решение, для которого все базисные переменные принимают неотрицательные значения.

Число допустимых базисных решений конечно и все они удовлетворяют ограничениям исходной задачи. Среди этих решений находится оптимальное (max), которое необходимо найти в процессе решения задачи ЛП.

Дата добавления: 2014-08-04; просмотров: 828; Нарушение авторских прав

Мы поможем в написании ваших работ!