Основные положения теории подобия

При расчете и проектировании теплообменных устройств, как правило, требуется рассчитать тепловой поток при конвективной теплоотдаче от флюида к стенке или, наоборот, от стенки к флюиду. Как мы уже знаем (см. раздел 1 курса), в этом случае тепловой поток находят по закону теплоотдачи, который в 1701 году предложил великий английский ученый Исаак Ньютон

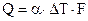или ,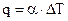

где 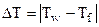– модуль разности температур между стенкой и флюидом, ^оС (К); ); T_w – температура поверхности теплообмена (стенки), ^оС (К); T_f – температура текучей среды (флюида) вдали от стенки, ^оС (К);Q – тепловой поток, Вт; q = Q/F – поверхностная плотность теплового потока, Вт/м²; F – площадь поверхности теплообмена (площадь поверхности стенки), м²; a – средний коэффициент теплоотдачи, Вт/(м²×К.

При заданных геометрических размерах системы теплообмена, температурах стенки и текучей среды задача расчета теплового потока сводится к определению коэффициента теплоотдачи (a). Заметим, что коэффициент теплоотдачи 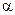не имеет физического смысла и выступает в роли коэффициента пропорциональности в законе теплоотдачи Ньютона. Из анализа закона Ньютона следует, что 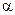численно равен тепловому потоку с 1 м² поверхности теплообмена при 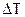между стенкой и текучей средой в 1^оС (К).

Коэффициент теплоотдачи находят, используя закон Ньютона, определив экспериментально тепловой поток и разность температур

.

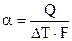Однако для сложных систем теплообмена необходимо, в принципе, выполнить бесконечное множество экспериментов, поскольку коэффициент теплоотдачи зависит в общем случае от координат, скорости, температуры, физических свойств среды и т.д.:

.

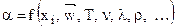Для уменьшения числа независимых переменных была разработана теория подобия. Теория подобия также дает правила моделирования и позволяет распространить результаты ограниченного числа экспериментов на группу подобных явлений. Теория подобия базируется на трех положениях теоремы Кирпичева-Гухмана:

1. Подобные процессы должны иметь одинаковую физическую природу.

2. Должно выполняться подобие условий однозначности, а именно: геометрическое подобие, кинематическое подобие (подобие скоростей), динамическое (подобие сил), тепловое подобие (подобие тепловых потоков).

3. В модели и объекте моделирования (образце) определяющие критерии должна быть равны. В этом случае равны и определяющие критерии.

Критерий – безразмерный комплекс, который характеризует отношение физических эффектов, но не является этим отношением. Другими словами критерий представляет собой меру отношения физических эффектов. Определяемые критерии также называют числами подобия.

Все критерии можно разделить на две основные группы: определяемые и определяющие. Определяемые критерии находят из эксперимента, а от определяющих критериев зависит результат эксперимента. Существует и группа независимых критериев или параметров, к которым следует отнести безразмерные координаты и безразмерное время. Однако в обратных задачах конвективного теплообмена безразмерное время может быть определяемым критерием.

Любая комбинация критериев является тоже критерием.

Если процесс течения и теплообмена не зависит от какого-либо критерия, то этот процесс называют автомодельным (независимым) по отношению к этому критерию.

Определяемые критерии конвективного теплообмена

Пусть флюид (f) омывает стенку произвольной формы (w). Вблизи стенки возникают гидродинамический и тепловой пограничные слои. Внутри гидродинамического пограничного слоя скорость флюида уменьшается от скорости невозмущенного потока (w₀) до нуля на стенке (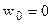) в силу условия прилипания. В тепловом пограничном слое происходит изменение температуры от T₀ – температуры за пределами пограничного слоя до T_w – температуры стенки. Пограничный слой имеет сложную структуру, которая описана в специальной литературе, например []. Для нас важно, что в области теплового пограничного слоя, непосредственно примыкающей к стенке, теплота передается только теплопроводностью. Тогда по закону Фурье:

,

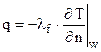где 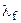– коэффициент теплопроводности текучей среды.

Наиболее часто в инженерных расчетах конвективного теплообмена для расчета безразмерного коэффициента теплоотдачи используют критерий Нуссельта (Нуссельт) и критерий Стантона (Стантон).

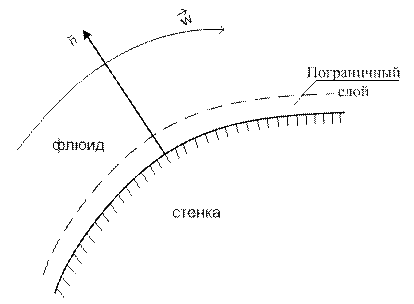
Рис. 6.1. К выводу критерия Нуссельта

Нуссельт характеризует отношение двух форм записи теплового потока, которым обмениваются флюид и стенка. Получим число Nu как отношение тепловых потоков:

,

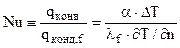где 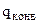– плотность теплового потока конвективной теплоотдачей, рассчитываемая по закону теплоотдачи Ньютона, а 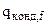– плотность теплового потока кондукцией в теплопроводной части пограничного слоя, рассчитываемая по закону Фурье. Учитывая, что градиент температур (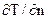) прямо пропорционален отношению (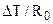) окончательно получим выражение критерия Нуссельта:

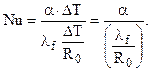
где R₀ – определяющий или характерный размер в системе теплообмена; 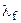– коэффициент теплопроводности текучей среды.

КритерийНуссельта характеризует отношение интенсивности конвективного теплового потока (α) к интенсивности теплообмена кондукцией в слое текучей среды вблизи стенки ().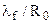

Без вывода запишем критерийСтантона или Стантон:

,

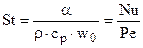где 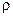– плотность флюида, кг/м³; с_р – изобарная теплоемкость, Дж/(кг×К); Pe – критерийПекле – критерий теплового подобия.

К группе определяемых критериев также относят критерийЭйлера (безразмерную силу давления) или Эйлер:

,

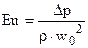который характеризует отношение силы давления к силе инерции или отношение энергии давления к кинетической энергии потока.

Замечание. Формально запись критерия Нуссельта и критерия Биó совпадают. Действительно: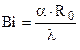– критерий Биó и 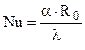– критерий Нуссельта.

Однако можно выделить три принципиальных отличия этих критериев подобия:

— во-первых, Биó относится к группе определяющих критериев, а Нуссельт – к группе определяемых критериев;

— во-вторых, в критерий Биó входит коэффициент теплопроводности твердого тела, а в критерий Нуссельта коэффициент теплопроводности текучей среды;

— в-третьих, определяющие размеры 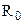, входящие в оба критерия имеют разный смысл и разное значение, поскольку характеризуют разные расчетные области теплообмена.

Определяющие критерии конвективного теплообмена

Для вывода определяющих критериев конвективного теплообмена, запишем систему дифференциальных уравнений конвективного теплообмена в векторной форме:

;

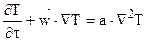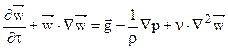
Зададим базовые или определяющие параметры расчетной области конвективного теплообмена, которые характеризуют условия однозначности краевой задачи конвективного теплообмена:

— определяющий размер – ;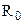

—время процесса в нестационарных задачах конвективного теплообмена – ;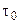

— определяющую температуру – ;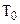

— определяющую скорость – ;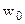

— давление флюида – ;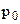

— физические свойства флюида, взятые из справочника при определяющей температуре (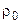– плотность, 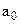– коэффициент температуропроводности, 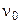– кинематический коэффициент вязкости).

Критерии теплового подобия получим отношением всех слагаемых уравнения Фурье-Кирхгофа к диффузионному члену уравнения, который моделирует перенос теплоты теплопроводностью или кондукцией. Отношение локального теплового потока, который характеризует изменение энтальпии элементарного объема, к кондуктивному тепловому потоку дает:

,

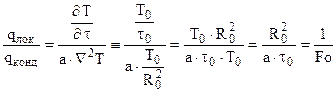где 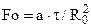– критерий Фурье – безразмерное время в задачах теплообмена.

Отнесем конвективный тепловой поток к кондуктивному тепловому потоку и получим определяющий критерий теплового подобия – критерий Пеклé:

.

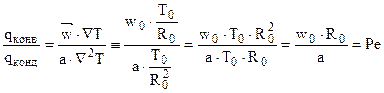Т.о. критерий Пеклé характеризует отношение теплового потока, переданного конвекцией к кондуктивному тепловому потоку в данной расчетной области теплообмена.

Критерии гидродинамического подобия получим отношением всех членов уравнения Навье-Стокса к конвективному члену уравнения, который моделирует силу инерции.

Найдем отношение локальной силы к силе инерции:

,

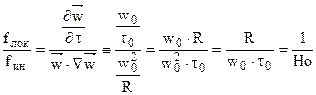где 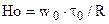– критерийгомохронности (однородности во времени) – характеризует отношение силы инерции к локальной силе (безразмерное время в задачах движения текучей среды).

Три силы, стоящие в правой части уравнения Навье–Стокса (f_g, f_p, f_тр) также отнесем к силе инерции. Получим:

;

;

.

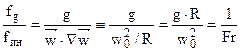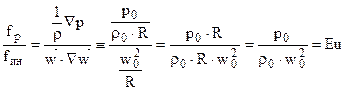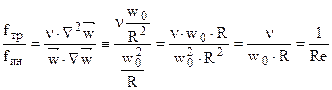В вышеприведенных формулах:

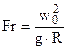– критерий Фруда или Фруд– характеризует отношение силы инерции к объемной силе (силе тяжести или гравитационной силе);

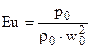– критерийЭйлера или Эйлер– характеризует отношение силы давления к силе инерции;

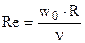– критерийРéйнольдсаили Рéйнольдс(критерий динамического подобия) – характеризует отношение сил инерции и сил трения. По значению критерия Re судит о режиме течения флюида при вынужденной конвекции.

В правой части уравнений Навье-Стокса стоят три критерия: Fr, Eu и Re, из которых два критерия однозначно определяют третий. При моделировании, как правило, cчитают Fr и Re определяющими критериями, а Eu – определяемым критерием.

При решении задач теплообмена при свободной конвекции скорость течения флюида определить довольно сложно, поэтому ее исключают из критериев подобия и учитывают косвенно расчетом гравитационной силы, возникающей из-за переменного поля плотности в неоднородном поле температур. В этом случае используют критерии Галлилея (Ga), Архимеда (Ar), Грасгофа(Gr) и Рэлея(Ra).

Используя правило о том, что комбинация критериев представляет собой тоже критерий, получим:

,

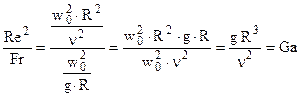где Ga – критерийГалилея, который характеризует отношение сил тяжести и сил вязкого трения:

.

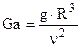Для учета свободной конвекции, возникающей из-за переменной плотности в данном объеме, умножим критерий Галлилея (Ga) на параметрический критерий 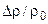и получим критерий Архимеда:

,

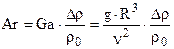где 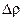– изменение плотности флюида, а 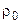– значение плотности при определяющей температуре.

Физический смысл критерия Архимеда заключается в том, что он представляет меру отношения подъемной силы из-за разности плотностей к силе вязкого трения.

Если переменная плотность среды возникает вследствие процесса теплообмена, то 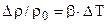и критерий Архимеда переходит в критерий Грасгофа:

,

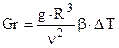где 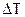– модуль разности температур между стенкой и флюидом, °C (K); 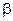– коэффициент объемного расширения флюида, 1/K.

Т.о. критерий Грасгофаявляется частным случаем критерия Архимедаи характеризует отношение термо-гравитационных сил и сил вязкого трения.

Замечание. Коэффициент объемного расширения капельных жидкостей приведен в справочниках в зависимости от температуры флюида, а для газов его рассчитывают по формуле:

,

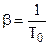где 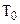– определяющая температура в Кельвинах!

По величине критерия Gr судят о режиме течения в задачах теплообмена при свободной конвекции для конкретного единственного флюида.

Для обобщения экспериментальных данных о режиме течения флюидов разной физической природы используют критерий Рэлея:

,

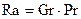где 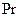– критерий Прандтля:

.

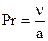КритерийПрандтля представляет собой отношение двух характеристик молекулярного переноса импульса (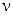) и теплоты (a) и является физическим параметром среды, значение которого приводят в справочниках в зависимости от температуры.

По величине критерия Прандтля (Pr) все текучие среды можно разделить на три группы:

— Pr << 1 – жидкие металлы;

— Pr 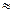1 – газы;

— Pr >> 1 – минеральные масла и органические жидкости.

Уравнения подобия

Функциональную связь между определяемыми и определяющими критериями называют уравнениями подобия. Для расчета безразмерного коэффициента теплоотдачи – критерия Нуссельта в стационарных задачах конвективного теплообмена используют следующие уравнения подобия:

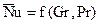– свободная конвекция;

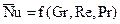– вынужденная конвекция (ламинарный режим течения);

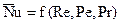– вынужденная конвекция (переходный и турбулентный режимы течения),

где 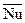– среднее по всей поверхности теплообмена значение критерия Нуссельта.

Уравнения подобия получают в два этапа. На первом этапе строят физическую модель процесса, соблюдая правила моделирования, и выполняют эксперимент на модели. В модели и объекте моделирования добиваются равенства определяющих критериев. Например:

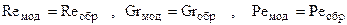и т.д.,

где индекс "мод" означает "модель", а индекс "обр" – "образец" или объект моделирования.

На втором этапе моделирования выполняют статистическую обработку результатов эксперимента, рассчитывают коэффициент теплоотдачи по закону Ньютона и получают конкретный вид уравнений подобия или т.н. критериальные уравнения, используя правило теории подобия:

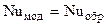или .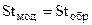

При построении модели и обработке результатов эксперимента в виде критериальных формул необходимо задать определяющие параметры, которые прямо или косвенно входят в критерии подобия. В стационарных задачах конвективного теплообмена к определяющим параметрам относят: определяющий размер (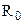), определяющую температуру (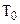) и в задачах вынужденной конвекции – определяющую скорость (w₀). Теория подобия не дает однозначного ответа на вопрос: "Какие величины принимать в качестве определяющих параметров?" Поэтому эту задачу решает сам ученый – автор критериального уравнения.

В качестве определяющего размера принимают тот размер системы конвективного теплообмена, от которого зависит конвекция. Например, при свободной конвекции около вертикальных поверхностей в качестве 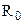логично принять высоту объекта (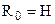), а при вынужденном течении в трубах – внутренний диаметр трубы ().

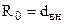В качестве определяющей температуры, как правило, принимают температуру, которую несложно измерить или рассчитать. За определяющую температуру чаще всего принимают средние температуры в системе теплообмена (в трубах и каналах, в трубных пучках и т.д.) – 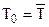, температуру флюида за пределами теплового пограничного слоя – 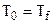и среднюю температуру пограничного слоя – .

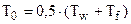Определяющую скорость находят из уравнения неразрывности:

,

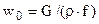где G – расход флюида, кг/c; 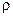– плотность, кг/м³; f – площадь поперечного сечения для прохода теплоносителя, м².

Внимание! При использовании критериальных уравнений определяющие параметры необходимо принимать точно так же, как это сделал автор формулы. Назначенные автором характерные или определяющие параметры 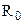, 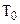и 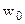указывают в комментариях к критериальной формуле.

Конкретный вид функциональной зависимости в уравнениях подобия задает ученый – автор формулы. В принципе для аппроксимации экспериментальных данных можно использовать любую полиноминальную зависимость. В отечественной литературе, как правило, в качестве аппроксимирующих уравнений применяют степенные функции вида:

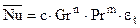— – свободная конвекция;

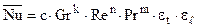— – вынужденная конвекция (ламинарный режим течения);

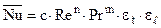— – вынужденная конвекция (переходный и турбулентный режимы течения),

где с, n, m, k – эмпирические коэффициенты, которые находят путем статистической обработки экспериментальных данных по методу наименьших квадратов;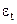– поправка, учитывающая зависимость физических свойств флюида от температуры; 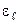– поправка, учитывающая влияние начального участка стабилизации потока.

Дата добавления: 2014-03-11; просмотров: 1182; Нарушение авторских прав

Мы поможем в написании ваших работ!