Линейные дифференциальные уравнения первого порядка

Определение 2. Линейным дифференциальным уравнением первого порядка называется уравнение

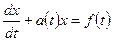, (3.1)

где 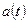,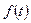- заданные функции времени .

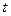Если 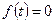при всех 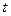, то уравнение называется однородным, в противном случае оно называется неоднородным. Если коэффициент 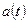постоянный, то (3.1) называют уравнением с постоянными коэффициентами.

Прежде чем решать уравнение (3.1) отметим свойство линейных однородных уравнений. Пусть 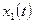и 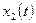- решения уравнения 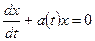. Тогда также является решением при любых значениях постоянных 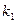и 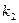. Действительно, подставив 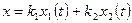в (3.1) получим:

Рассмотрим однородное уравнение

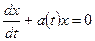. (3.2)

Чтобы решить это уравнение, запишем его в виде:

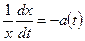или .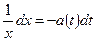

Учитывая, что 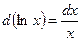, имеем: .

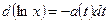Интегрируя обе части последнего выражения, получим:

, , ,

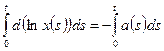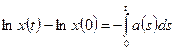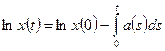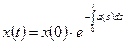. (3.3)

Формула (3.3) дает решение уравнения (3.2) с начальным условием .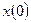

Пример 4. Популяция бактерий увеличивается таким образом, что удельная скорость роста в момент (время выражается в часах) составляет величину 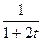. Пусть начальная популяция 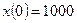. Какой будет популяция после 12 ч. роста?

Решение: По условию удельная скорость равна 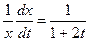. Это однородное линейное уравнение первого порядка при 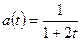. Интегрируя его, получаем:

.

, .

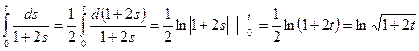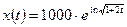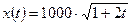Размер популяции после 12ч. роста выражается величиной

.

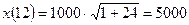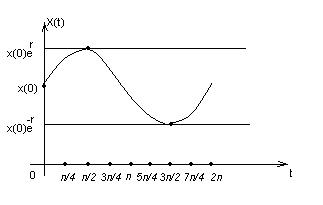
Пример 5. Модель сезонного роста.

Дифференциальное уравнение первого порядка 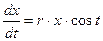, где 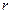- положительная постоянная, можно рассматривать как простейшую модель сезонного роста. Скорость роста 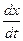популяции 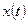становится то положительной, то отрицательной, и популяция то возрастает, то убывает. Это может вызываться такими сезонными факторами, как доступность пищи.

Заметим, что здесь .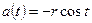

Так как 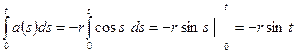, то общее решение записывается в виде: .

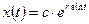Полагая 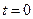, получим 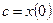, т.е. размер популяции в момент 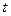есть 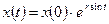. Максимальный размер популяции, равный 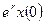, достигается при 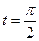,,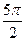,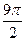…, когда 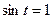. Минимальный размер, равный 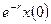, достигается при 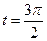,,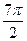,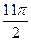…, когда 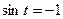. В этой модели размер популяции колеблется от 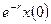до 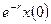с периодом 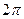. Моменты времени 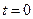,,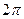,… можно считать серединами сезонов наибольшей доступности пищи (летних сезонов),а моменты 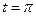,,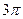,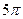… соответствует серединам сезонов наибольшей нехватки пищи (зимних сезонов). Продолжительность одного года соответствует 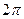ед. времени.

Дата добавления: 2014-03-11; просмотров: 689; Нарушение авторских прав

Мы поможем в написании ваших работ!