
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Выбор порядка тригонометрического полинома
Выбор основывается на представлении функции тригонометрическим полиномом некоторого порядка. Под порядком тригонометрического полинома будем понимать количество гармоник, используемых при аппроксимации m = m0 ³ 1.
Будем считать, что ошибки измерения носят случайный характер с нормальным законом распределения N (0, s2). Ошибки измерений независимы, а значения аргумента равноотстоящие, т.е. дискретизация аргумента равномерная.
Тогда ошибки параметров aj и bj будут также распределены по нормальному закону распределения с удвоенной дисперсией.
N (0, 2s2), j = 1, 2, 3, N (0, 4s2), j = 0.
Для МНК можно записать
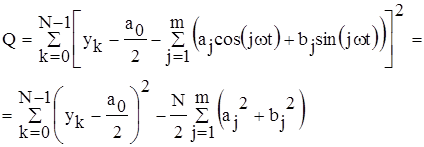
т.е. увеличивая порядок полинома на 1 , мы уменьшаем остаток на величину
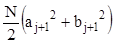 .
.
Значение отношения 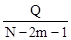 , где N-2m-1 - степень свободы, является несмещенным, состоятельным и эффективным. Q - среднеквадратическое отклонение
, где N-2m-1 - степень свободы, является несмещенным, состоятельным и эффективным. Q - среднеквадратическое отклонение
Можно считать, что при достаточно больших значениях выборки N
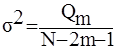 .
.
На основе приведенной дисперсии можно определить стратегию введения дополнительных компонентов ряда. Обычно наблюдается следующая ситуация: с увеличением порядка аппроксимирующего ряда дисперсия убывает на одном участке достаточно быстро, а на другом участке медленно, и поэтому в рамках заданной точности можно уменьшить количество элементов со второго участка, незначительно увеличивая погрешность аппроксимации. Потому в рамках заданной точности можно выбрать порядок (число гармоник) аппроксимирующего полинома; чаще всего приходится решать другую задачу. Найти такой минимально возможный порядок аппроксимирующего ряда, чтобы, незначительно уступая в погрешности, получить наиболее компактную форму аппроксимирующего ряда, т.е. повышать порядок полинома необходимо до какого-то значения. Рис.4.2 иллюстрирует разбиение всего множества полученных коэффициентов ряда на существенные и несущественные, которыми можно пренебречь с потерей некоторой точности. На рис. 4.2 в качестве величины d используется расстояние между среднеарифметическими значениями коэффициентов в группировках.
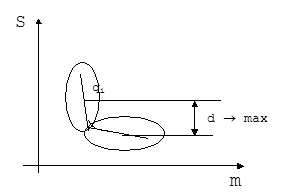
Рис 4.2 Иллюстрация выбора существенных коэффициентов.
Математически выбор осуществляется по следующей формуле
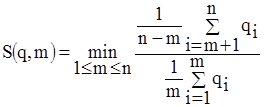 ,
,
где 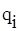 - вес i-той гармоники.
- вес i-той гармоники.
Пример расчета порядка полинома.
Пусть заданы значения аргумента и функции
| К | X | y |
| 3.0004 | ||
| 1h | 5.7203 | |
| 2h | 3.1993 | |
| 3h | - 1.0981 | |
| 4h | - 0.8676 | |
| 5h | 2.9890 | |
| 6h | 4.0985 | |
| 7h | 1.1477 |
Воспользовавшись формулой для выбора порядка полинома получим
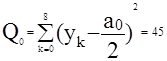 ;
;
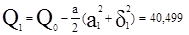 ;
;
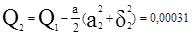 ;
;
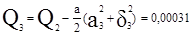 .
.
Третья гармоника не увеличивает точность моделирования. Следовательно, аппроксимирующую функцию можно представить
y=2+cos(wt)+3sin(2wt) .
Из анализа видно, что достаточно выбрать две гармоники. Значит модель сильно упрощается.
4.3 Вопросы для самоконтроля
1. Перечислите модели представления временных сигналов.
2. Дайте определение ортогонального функционального ряда.
3. Какие ряды обладают свойством ортогональности?
4. В чем заключается смысл аппроксимации?
5. Чем определяется выбор порядка аппроксимирующего полинома?
6.Есть ли связь между порядком полинома и количеством экспериментальных дискрет при аппроксимации рядом Тейлора, тригонометрическим полиномом?
7.Как можно определить минимально возможный порядок аппроксимирующего полинома?
| <== предыдущая страница | | | следующая страница ==> |
| Аппроксимация тригонометрическим полиномом | | | Моделирование электрических СИСТЕМ |
Дата добавления: 2014-08-04; просмотров: 625; Нарушение авторских прав

Мы поможем в написании ваших работ!