Аппроксимация тригонометрическим полиномом

Рассмотрим тригонометрический полином (ряд Фурье):

;

,

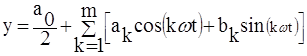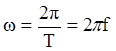где f - Гц ; w - рад. (В языке программирования Паскаль и MATHCAT используется частота, измеряемая в радианах).

Система функций представляет следующий ряд:

cos(wt), sin(wt), . . . cos(kwt), sin(kwt).

Обычно аргумент времени пишут в следующем виде:

,

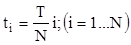где T - период, N - величина выборки.

Система функций является ортогональной, так как она удовлетворяет следующим условиям:

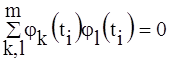, k ¹ l.

Ряды тригонометрические, Чебышева, Лагерра являются ортогональными. Широко используемый ряд Тейлора не ортогонален.

Свойство ортогональности учитывают при оценивании коэффициентов для упрощения вычислительных процедур. Пересчет коэффициентов не осуществляется при введении дополнительных элементов ряда. В силу ортогональности тригонометрического ряда параметры ряда можно вычислить по следующим формулам:

,

,

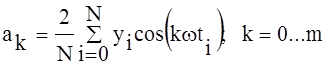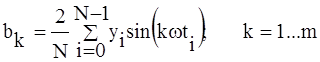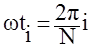
В вычислении часто используют рекуррентную форму подсчета коэффициентов.

Дата добавления: 2014-08-04; просмотров: 666; Нарушение авторских прав

Мы поможем в написании ваших работ!