МОДЕЛИРОВАНИЕ СИГНАЛОВ ВО ВРЕМЕННОЙ ЗАВИСИМОСТИ

Пусть дана выборка y₁, t₁; y₂, t₂ . . . y_n, t_n, представляющая зависимость некоторой переменной у от времени t (рис.4.1).

Рис 4.1 График временной функции

Будем использовать аппроксимацию - метод приближения любой аналитической функции к данной выборке. Примерами приближения могут быть следующие функции:

y = a + bt ;

y = a e^{-bt ;}

y = a sin ( w t ) .

Если выбрана зависимость, то по данным выборки задача аппроксимации сводится к оценке коэффициентов аналитической функции, в противном случае необходимо пользоваться одним из рядов аппроксимации (ряд Фурье, ряд Тейлора, ряд Чебышева и т.д.) либо методом подбора аналитической функции, т.е. подбирать и оценивать наиболее “удачную“ функцию. Последняя задача относится к задаче структурной идентификации

Пусть в общем виде дана функция y = f (a ₁ , a₂ . . х, t), тогда на основе МНК

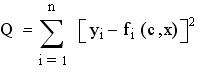
можно перейти к оцениванию коэффициентов и далее проверке адекватности модели.

Хотя среди методов и критериев аппроксимации наибольшее распространение получил метод МНК, в ряде случаев можно использовать абсолютную величину отклонения - abs(Q), третий, четвертый порядки отклонений модели или композиции этих критериев. Наиболее мощным критерием аппроксимации считается метод максимума правдоподобия, который в основном используется при статистической обработке данных. МНК распространен из-за его аналитичности и достаточно простой математической обработки данных.

Дата добавления: 2014-08-04; просмотров: 329; Нарушение авторских прав

Мы поможем в написании ваших работ!