Моделирование электрических СИСТЕМ

5.1 Основы моделирования электрических систем

Рассмотрим систему как соотношение входного сигнала, выходного сигнала и передаточной функции системы.

Имеем 3 задачи:

1) определение выходного сигнала по известному входному и известной передаточной функции:

y(t)=F(x(t),W);

2) определение входного сигнала по известному выходному сигналу и известной передаточной функции:

x(t)=F(y(t),W);

3)определение передаточной функции по известным входным и выходным сигналам:

W=F(x(t),y(t)).

Например:

;

;

.

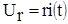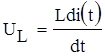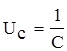В электрических цепях для решения этих задач нужно составлять интегродифференциальные уравнения, например:

,

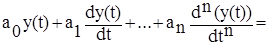
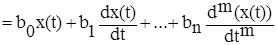В последнем уравнении x(t) - входной сигнал, y(t) - выходной сигнал,a₀… a_n, b₀… b_n – коэффициенты уравнения.

Коэффициенты a и b зависят от внутренней структуры системы и операций в этой системе и определяются ее параметрами, конкретными элементами электрической системы: сопротивлениями, емкостями, индуктивностями и т.д.

Коэффициенты не зависят от входного и выходного сигналов.

В виде набора коэффициентов исследовать систему затруднительно, поэтому если привести дифференциальное уравнение с помощью преобразования Лапласа к виду y(p)=W*x(p), где p - комплексная переменная, то получим передаточную функцию:

.

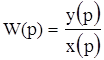Обычно передаточные функции рассматриваются в частотной области в виде

W(jω)=P(ω)+jQ(ω)=A(ω)e^-jω_.

Чаще всего передаточную функцию анализируют по амплитудно-частотной характеристике

,

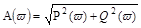и фазочастотной характеристике:

,

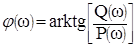Содержательный смысл амплитудно-частотной характеристики: отношение выходного сигнала к входному при разных частотах

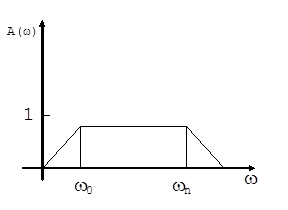
Рис. 5.1 Амплитудно-частотная характеристика

Амплитудно-частотная характеристика для разомкнутых систем без автогенерации всегда меньше единицы. Если на вход подается единичный сигнал, то, проходя через систему, часть энергии рассеивается, при этом подразумевается, что в системе нет дополнительных источников энергии.

Фазочастотная характеристика показывает изменение фазы входного сигнала в выходном в зависимости от частоты.

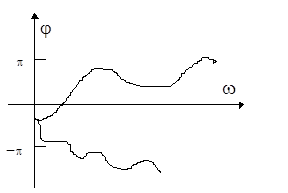
Рис. 5.2. Пример фазочастотной характеристики

Обычно амплитудно-частотную характеристику представляют в логарифмическом масштабе в силу достаточно большого диапазона частот, применяя операцию логарифмирования получим:

.

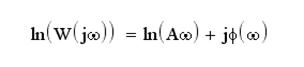Логарифмическая амплитудно-частотная характеристика имеет вид:

,

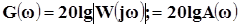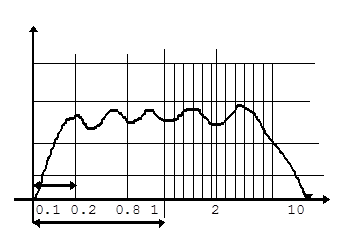
Рис. 5.3. Логарифмическая амплитудно-частотная характеристика

Отношение в передаточных функциях вводится по амплитуде и характеризует линейные отношения первого порядка.

Обычно рассматривают отношения мощностей (второго порядка).

Для оценивания отношения мощностей вводится единица измерения - Белл. Но чаще используют 1/10 Белл = децибел.

, .

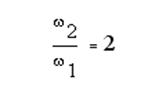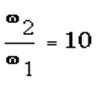Амплитудно-частотную характеристику можно найти посредством преобразования Лапласа. Такой подход используют в связи с тем, что для инженерных расчетов решение дифференциальных уравнений достаточно затруднено.

Поэтому разработан математический аппарат на основе преобразования Лапласа, позволяющий свести решение дифференциального уравнения к решению алгебраического уравнения.

Всякое обыкновенное дифференциальное уравнение имеет решение в виде суммы экспонент:

,

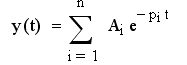где p_i - корни характеристического уравнения, n – порядок дифференциального уравнения.

Характеристические уравнения составляются на основе коэффициентов дифференциального уравнения. Характеристическое уравнение можно получить на основе передаточной функции, приравняв знаменатель этой функции к нулю. При этом информация о структуре исследуемой системы передается полностью в виде коэффициентов уравнений.

Формальность перехода от временного аргумента в дифференциальных уравнениях к комплексному аргументу в передаточной функции заключается в том, что вместо операции дифференцирования производится подстановка комплексной переменной P.

;

;

;

.

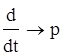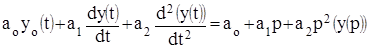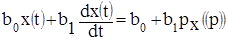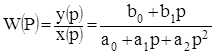Преобразования Лапласа позволяют вместо решения дифференциальных уравнений решать алгебраические уравнения соответствующего порядка.

Между преобразованиями Фурье, преобразованиями Лапласа и временной областью существует треугольник преобразований.

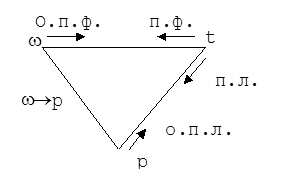
Рис. 5.4. Треугольник соотношений временного,

частотного и комплексного аргументов

На рис.5.4 обозначено:

t®w - прямое преобразования Фурье (переход аргумента исследуемой функции от временной области в частотную);

w®t - обратное преобразование Фурье (переход аргумента исследуемой функции от частотной области в временную область);

t®p- преобразования Лапласа (переход аргумента исследуемой функции из временной в комплексную область);

p®t - обратное преобразование Лапласа (из комплексной в временную );

w®p - формальная замена аргументов w на p (переход аргумента исследуемой функции из частотной в комплексную; p - комплексное число).

Дата добавления: 2014-08-04; просмотров: 441; Нарушение авторских прав

Мы поможем в написании ваших работ!