
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Основные понятия. Дифференциальные уравнения
Дифференциальные уравнения.
Лекция 10 - 11
План лекции.
1. Основные понятия и определения
2. Классификация дифференциальных уравнений и способы их решения.
Уравнение вида
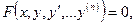 (1)
(1)
связывающее аргумент х, неизвестную функцию  и её производные, называется обыкновенным дифференциальным уравнением (ОДУ).
и её производные, называется обыкновенным дифференциальным уравнением (ОДУ).
В явной форме оно разрешено относительно старшей производной
 (2)
(2)
Решить дифференциальное уравнение (ДУ) – это значит найти все неизвестные функции, обращающие уравнение в тождество. Такая задача называется интегрированием дифференциального уравнения. График решения называется интегральной кривой.
Решение ДУ без дополнительных условий является неоднозначным, и оно описывает целое семейство интегральных кривых на плоскости. Для однозначного решения ОДУ n-го порядка надо задать дополнительно n условий. Обычно это значение функции 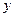 и её производных до (n-1)-го порядка включительно при некотором заданном значении переменной х.
и её производных до (n-1)-го порядка включительно при некотором заданном значении переменной х.
Общее решение ОДУ n-го порядка
 (3)
(3)
является функцией переменной х и n произвольных констант С1, С2, …, Сn.
Частное решение ОДУ получается при подстановке в общее решение некоторых конкретных числовых значений С1, С2, …, Сn.
Пример. Решить уравнение 
Исходное уравнение равносильно равенству 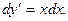 Интегрирование приводит к выражению:
Интегрирование приводит к выражению:  Повторное интегрирование приводит к выражению:
Повторное интегрирование приводит к выражению:  Это общее решение.
Это общее решение.
Частное решение может быть таким: при условиях 
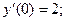

| <== предыдущая страница | | | следующая страница ==> |
| Несобственные интегралы | | | ДУ 1-го порядка. Теорема о существовании и единственности решения |
Дата добавления: 2014-02-28; просмотров: 486; Нарушение авторских прав

Мы поможем в написании ваших работ!