Несобственные интегралы

Пусть функция 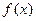определена и интегрируема на произвольном отрезке 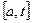, т.е. функция

определена для произвольного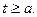

Несобственным интегралом 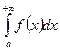от функции 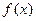на полуинтервале 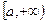называется предел функци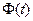и при 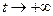, т.е.

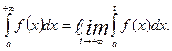
Если предел существует и конечен, то несобственный интеграл называется сходящимся, в противном случае – расходящимся.

Аналогично определяется несобственный интеграл на полуинтервале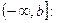

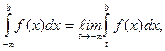
а также понятие его сходимости.

Пусть для некоторого 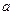несобственные интегралы 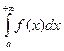и сходятся. Тогда

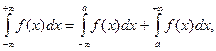
при этом интеграл 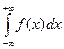называется сходящимся. Если хотя бы один из интервалов, входящих в правую часть, расходится, то несобственный интеграл в левой части называется расходящимся.

Пусть функция 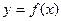непрерывна, но не ограничена на полуинтервале 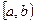. Если существует и конечен предел 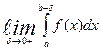, где 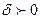, то он называется несобственным интегралом от функции 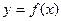на 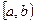и обозначается , т.е.

.

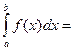
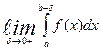В этом случае данный несобственный интеграл называется сходящимся, в противном случае – расходящимся. Аналогично вводится понятие несобственного интеграла от функции 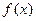, непрерывной, но не ограниченной на

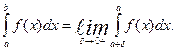
Приближенное вычисление определённых интегралов.

Использование формулы Ньютона-Лейбница не всегда возможно, поскольку не всегда можно найти первообразную подынтегральной функции. Поэтому на практике используются так называемые численные методы, позволяющие найти приближённое значение интеграла с требуемой точностью. Такой подход предпочтителен ещё и потому, что возможности вычислительной техники непрерывно возрастают.

Рассмотрим один из таких методов – формулу трапеций. Пусть на 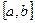задана непрерывная неотрицательная функция 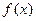. Тогда, если отрезок 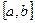разбить на 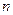равных отрезков, каждый длиной 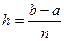, формула трапеций имеет вид:

,

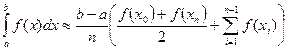где , , ;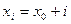

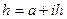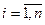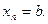
Погрешность формулы трапеций равна

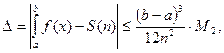
где S(n) – правая часть формулы трапеций,

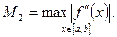Формула трапеций тем точнее, чем меньше шаг разбиения h.

Вопросы для самоконтроля:

1. Применение формулы Ньютона-Лейбница

2. Приближенное вычисление определенного интеграла.

Дата добавления: 2014-02-28; просмотров: 576; Нарушение авторских прав

Мы поможем в написании ваших работ!