Теорема Пуассона

Пусть событие А - маловероятное, тогда вероятность его наступления при каждом испытании близка к нулю. В этом случае даже при большом числе испытаний 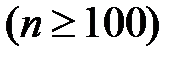по небольшой величине произведения np расчеты вероятностей 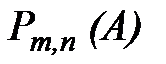по формуле Муавра - Лапласа оказываются недостаточно точными. В таких случаях следует применять другую асимптотическую формулу - формулу Пуассона.

Теорема.Если вероятность р наступления события А при каждом испытании постоянна, но близка к нулю, число независимых испытаний n достаточно велико, а произведение np остается небольшим, то вероятность того, что событие А наступит m раз, приближенно равна

, где

Доказательство. Действительно, пусть проводится n независимых испытаний, в результате которых событие А наступает с постоянной вероятностью р при каждом испытании. Вероятность наступления события А m раз при этих испытаниях найдем по формуле Бернулли

По условию теоремы a=np, отсюда p=a/n.

Тогда .

Запишем это равенство в таком виде

Так как по условию теоремы n достаточно велико, то множители 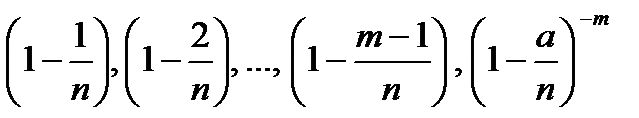приближенно можно считать равными 1. Тогда, заменяя их в предыдущем равенстве единицей, получим приближенное значение 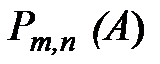, а именно:

.

Известно, что (следствие из второго замечательного предела). Тогда при достаточно больших n имеем . Используя этот результат, получаем асимптотическую формулу расчета вероятности , называемую формулой Пуассона

, где

Вычисления P_m,n(A) по формуле Пуассона дают незначительную погрешность при выполнении следующего условия:a=np≤10. Для упрощения расчетов по рассматриваемой формуле составлена таблица ее значений (прил. 3).

Дата добавления: 2014-09-01; просмотров: 448; Нарушение авторских прав

Мы поможем в написании ваших работ!