Определение числа корней алгебраических уравнений

Пусть дано уравнение

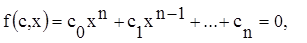(6.3)

где n-целое число, а коэффициенты c₀…c_n- действительные числа. Часто до вычисления значений корней ставится задача определить количество этих корней уравнения (6.3), определить их тип значений (действительные или комплексные), определить максимальное значение корня или области значений корней.

Такой интерес к решению алгебраических уравнений и к характеристикам корней проявляется не только в изучении корней как особенных точек алгебраических уравнений, но и в исследовании характеристических уравнений систем дифференциальных уравнений. Такие исследования занимают важное место в прикладных науках, например: в теории автоматического регулирования и управления. По корням характеристического уравнения можно определить устойчивость системы и косвенные характеристики переходного процесса

Самым простым способом определения действительных корней алгебраических уравнений является визуальное представление, т.е. представление функции в виде графика на достаточно большом или заранее заданном диапазоне изменения аргумента. С использованием средств компьютерной графики, например пакетом MATHCAD, такой подход можно реализовать и к трансцендентным уравнениям. Поэкспериментировав с величиной шага дискретизации и диапазоном табуляции, можно приближенно определить значение корней уравнения по моменту пересечения графика изучаемой функции с осью абсцисс (ось х-ов).

Однако такой путь неприемлем для нахождения комплексных корней и, тем более, для уравнений с комплексными коэффициентами. Поэтому приведем краткий обзор аналитических методов.

В основу всех методов заложена зависимость корней уравнения от коэффициентов алгебраического уравнения (6.3).

Общее число корней алгебраического уравнения равно наивысшей степени (порядка) полинома левой части уравнения. При этом в зависимости от значений коэффициентов корни могут быть действительными, комплексными, комплексно сопряженными, кратными и в различных этих сочетаниях.

Оценки корней действительных алгебраических уравненийЕсли коэффициенты алгебраического уравнения действительные числа, то при действительных значениях переменной х многочлен f(c,х) будет принимать действительные значения.

Все корни уравнения (6.3) по модулю не превосходят числа:

,

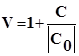где С - наибольшее число ряда 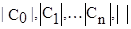- модуль числа.

Определение действительных корней. Согласно правилу знаков Декарта число положительных корней действительного алгебраического уравнения (6.3) либо равно числу К перемен знака в последовательности 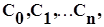коэффициентов (без учета нулевых коэффициентов), либо меньше числа К на четное число.

Следовательно, если коэффициенты уравнения знаки не меняют, то положительных корней нет.

Применяя это правило к f(c, -x), получаем аналогичный вывод для отрицательных корней.

Определение верхней границы значений действительных корней. Если первые К-коэффициенты 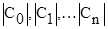действительного уравнения (6.3) неотрицательны (С_к - первый отрицательный коэффициент), то все положительные корни меньше

,

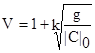где g-наибольшая из абсолютных величин отрицательных коэффициентов.
Для f(c, -x) этот результат верен для отрицательных корней.

Если имеется такое наименьшее значение V_r, при котором (x=V_r) -полином 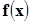и его производные 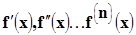принимают положительные значения, то V₁- является верхней границей действительных корней уравнения (6.3).

Согласно теореме Ролля производная 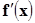действительного многочлена 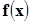имеет нечетное число действительных корней между двумя соседними действительными корнями многочлена .

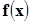Следующая теорема (теорема Бюдана-Фурье) позволяет определить количество корней уравнения (6.3) на интервале .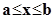
Если К(х) - число перемен знака в последовательности значений 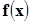, 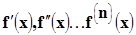для действительного алгебраического уравнения (6.3), то число действительных корней, заключенных между двумя действительными числами a и b (b>a), не являющимися корнями уравнения (6.3), либо равно (к(a)-к(b)), либо меньше этой разности на четное число.

При подсчете к(a) члены последовательности, равные нулю, вычеркиваются. При подсчете к(a) - нулевые члены 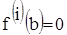для 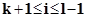заменяются на .

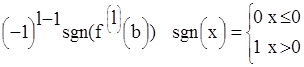Число действительных корней, заключенных между a и b, будет нечетно или четно в зависимости от того, будут ли значения 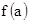и 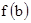иметь противоположные или одинаковые знаки.

Комплексные корни. Комплексные корни действительного алгебраического уравнения появляются парами комплексных сопряженных чисел. Действительное алгебраическое уравнение нечетной степени всегда имеет хотя бы один действительный корень.

Согласно теореме Рауса-Гурвица, число корней с положительной действительной частью действительного алгебраического уравнения (6.3) равно числу перемен знака в последовательности (g_i отлично от нуля):

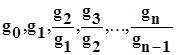,где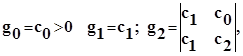

.

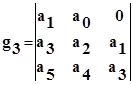
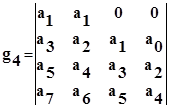Для того, чтобы все корни действительного уравнения (6.3) имели отрицательные действительные части, необходимо и достаточно, чтобы выполнялись неравенства.

,

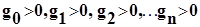где из положительности всех g_i следует положительность всех коэффициентов уравнения (6.3).

Теорема Рауса-Гурвича лежит в основе алгебраических критериев устойчивости, используемых при исследовании систем автоматического регулирования.

Дата добавления: 2014-08-04; просмотров: 901; Нарушение авторских прав

Мы поможем в написании ваших работ!