Решение систем дифференциальных уравнений

Для моделирования динамических систем используются математические модели в виде дифференциальных уравнений. Дифференциальные уравнения связывают функции с их производными, отражая динамические процессы, происходящие в исследуемой системе. Результатом решения дифференциальных уравнений являются функции, для отыскания которых используются более трудоемкие алгоритмы.

Численными методами решаются не только отдельные дифференциальные уравнения, но и их системы без значительного усложнения алгоритмов. Для дифференциальных уравнений высших порядков используется подстановка путем замены переменных для приведения их к первому порядку. Численные решения уравнений описаны и в учебниках, и в руководствах по MAHTCAD, поэтому ограничимся одним из методов.

Наиболее простой из методов решения дифференциальных уравнений – метод Эйлера, который требует записи в форме Коши, т.е. когда производная представлена в левой части уравнения:

.

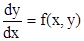Решением этого уравнения будет некоторая функция - y=f(x).

Итерационная процедура решения будет иметь вид

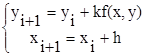i₀=0, x₀=0, y₀=0,

k, h – масштабирующие множители, шаги итерационной процедуры. Величины шагов теоретически обосновываются и определяются тем или иным методом.

Система дифференциальных уравнений может быть представлена в виде

- .

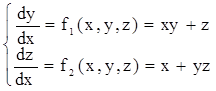Решением этой системы будут две функции, удовлетворяющие приведенной системе:

y=f₁(x, z), z=f₂(x,y).

Рекуррентные алгоритмы требуют задания начальных условий как для значений искомых функций, так и для значений производных. Обязательно должны указываться диапазон изменения аргументов и шаг дискретизации аргумента. Последний отвечает за точность решения задачи. Для оптимизации алгоритма шаг может выбираться адаптивными методами, что усложняет алгоритм, но значительно увеличивает его скорость сходимости.

Составив систему начальных значений, можно записать алгоритм решения системы дифференциальных уравнений:

.

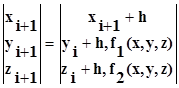Метод Эйлера наиболее прост в вычислительном плане, но уступает по точности современным методам.

Дата добавления: 2014-08-04; просмотров: 382; Нарушение авторских прав

Мы поможем в написании ваших работ!