Методы случайного поиска

Содержание метода заключается в генерировании случайных чисел (RND), которые распределены по равномерному закону плотности вероятности в диапазоне от нуля до единицы.

.

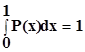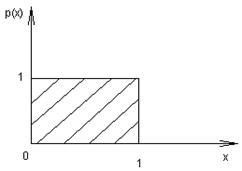
Рис 6.5. Поле генерации случайных чисел

Генераторы случайных чисел генерируют псевдослучайные числа. Поэтому если потребуется другой закон распределения, то можно воспользоваться нормальным законом:

.

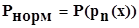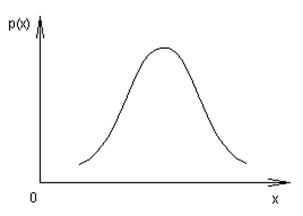
Рис 6.6. Кривая нормального распределения

После генерации случайных чисел они используются в следующих алгоритмах: нахождение корней алгебраических и трансцендентных уравнений, нахождение значений определённых интегралов, решение дифференциальных уравнений и их систем, поиска оптимальных значений в задачах оптимизации (в том числе оценивание коэффициента аппроксимирующих функций на основе метода наименьших квадратов).

Алгоритм метода случайного поиска основан на генерации большого количества случайных чисел. Подстановка этих чисел в алгоритм одной из перечисленных задач позволяет выбрать наилучшее решение, то есть реализуется случайный перебор различных решений, а на основе сравнения этих решений отбирается наилучшее. Теорема больших чисел доказывает, что при количестве экспериментов n®µ мы с достаточно большой вероятностью p®1 получим требуемое решение.

Метод решения алгебраических и трансцендентных уравнений. Пусть дана искомая функция на диапазоне от x_min до x_max: x=rnd.

Обычно функцию нормируют на диапазоне 0<x<1, 0<y<1 либо на генераторе случайных чисел указывают диапазон генерации чисел:

x=rnd(10);

x_max - x_min=10.

Суть метода: генерируется число x₁, от него вычисляется функция f₁(x₁), затем генерируется следующее число x₂ и от него вычисляется функция f₂(x₂), после чего f₁(x₁) и f₂(x₂) сравниваются между собой и из них выбирается меньшее значение. Так происходит до тех пор, пока на n-ом шаге .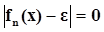

Недостаток метода случайного поиска заключается в том, что он долго сходится к решению задачи с повышенной заданной точностью.

Для дифференциальных уравнений итерационная запись алгоритма Эйлера сходится и для случайного поиска, но с тем отличием, что шаги по индексу i определяются с помощью генератора случайных чисел: x_i+1=rnd(i+1). Остановка происходит, когда значение y на i-ом шаге не отличается больше, чем на величину заданной точности.

çy_i+1-y_iç£e_y;

çz_i+1-z_iç£e_z;

çx_i+1-x_iç£e_{x; .}

Дата добавления: 2014-08-04; просмотров: 336; Нарушение авторских прав

Мы поможем в написании ваших работ!