
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дисперсия числа появлений событий в независимых испытаниях
|
Читайте также: |
Пусть производится n независимых испытаний, в каждом из которых вероятность появления события А постоянно.
Теорема 6.3. Дисперсия числа появлений события А в n независимых испытаниях, в каждом из которых вероятность Р появления события постоянно и равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании.
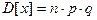
Мат. ожидание 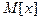 числа появления события А в n независимых испытаний равна произведению числа испытаний на вероятности появления и непоявления в одном испытании
числа появления события А в n независимых испытаний равна произведению числа испытаний на вероятности появления и непоявления в одном испытании 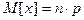 .
.
Доказательство: рассмотрим случайную величину Х– число появлений события А в n независимых испытаний. Очевидно, общее число появлений события А в этих испытаниях равно сумме появления событий в этих испытаниях. 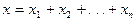 , где
, где 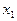 – число наступления событий в одном испытании и т.д. Величины
– число наступления событий в одном испытании и т.д. Величины 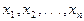 взаимонезависимы, поэтому
взаимонезависимы, поэтому 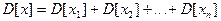 .
.
Вычислим 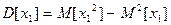 .
.
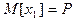 , так как
, так как 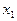 – число появлений события А в одном испытании.
– число появлений события А в одном испытании.
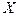
| ||
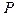
| 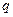
| 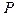
|
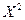
| 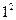
|
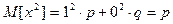
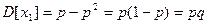
Аналогично можно вычислить 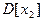 и т.д.
и т.д. 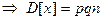
| <== предыдущая страница | | | следующая страница ==> |
| Свойства дисперсии | | | Среднеквадратичное отклонение |
Дата добавления: 2014-02-26; просмотров: 951; Нарушение авторских прав

Мы поможем в написании ваших работ!