
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Дисперсия дискретной случайной величины
Легко указать такие случайные величины, которые имеют различные возможные значения. Рассмотрим, например, дискретные случайные величины X и Y, заданные:
| X | -0.01 | 0.01 |
| P | 0.5 | 0.5 |
| Y | -100 | |
| P | 0.5 | 0.5 |
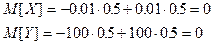
Таким образом зная лишь математическое ожидание случайной величины еще нельзя судить о том, какие возможные значения они могут принимать, и о том как они рассеяны, другими словами математические ожидания полностью ? ? ?
По этим причинам рядом с математическим ожиданием вводят другие характеристики. Так, например, для того, чтобы оценить как рассеяны возможные значения случайной величины пользуются исловой характеристикой, называемой дисперсией. Прежде всего введем понятие отклонения случайной величины от ее математического ожидания: пусть Х– случайная величина 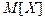 – ее математическое ожидание. Рассмотрим
– ее математическое ожидание. Рассмотрим 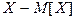 – новую случайную величину. Отклонением называется разность между случайной величиной и ее математическим ожиданием.
– новую случайную величину. Отклонением называется разность между случайной величиной и ее математическим ожиданием.
Пусть известен закон распределения случайных величины Х:
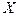
| 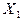
| 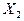 . . . . . .
| 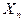
|
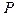
| 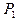
| 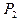 . . . . . .
| 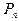
|
Напишем закон распределения отклонения. Для того, чтобы отклонение приняло значение 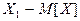 необходимо и достаточно, чтобы случайная величина приняла значения
необходимо и достаточно, чтобы случайная величина приняла значения 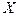 .
.
Верность этого события-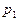 следует вероятность того,что отклонение примет значение
следует вероятность того,что отклонение примет значение 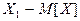 тоже равна
тоже равна 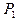 . Аналогично определяется и вероятности для остальных отклонений случайной величины. Таким образом отклонение имеет следующий закон распределения:
. Аналогично определяется и вероятности для остальных отклонений случайной величины. Таким образом отклонение имеет следующий закон распределения:
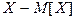
| 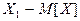
| . . . | 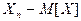
|
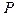
| 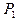
| . . . | 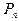
|
Теорема 6.1. Мат. ожидание 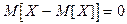 .
.
| <== предыдущая страница | | | следующая страница ==> |
| Лекция 6. Числовые характеристики дискретных случайных величин | | | Определение дисперсии и ее свойства |
Дата добавления: 2014-02-26; просмотров: 743; Нарушение авторских прав

Мы поможем в написании ваших работ!