Дисперсия. В определение среднего случайной величины

Среднее значение

В определение среднего случайной величины

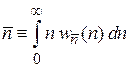
подставляем 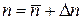. Получаем

,

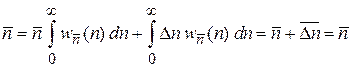где учтено условие нормировки

,

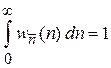и среднее отклонение от среднего . Следовательно, в распределении Гаусса (1.19а)

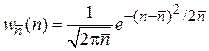
величина 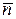является средним значением числа частиц n.

В определение дисперсии подставляем (1.19а)

.

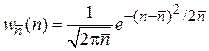заменяем 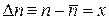, и находим

.

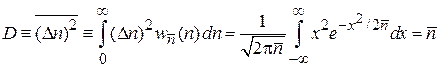Последний интеграл вычислен по формуле из курса ММФ

.

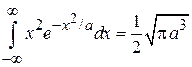Дисперсия

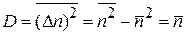(1.20)

совпадает с результатом (1.18б) для распределения Пуассона.

Из (1.19а) и (1.20) получаем плотность вероятности, выраженную через дисперсию

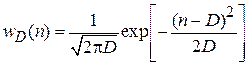. (1.21)

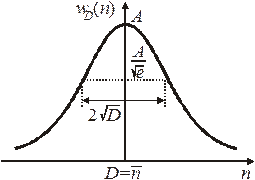
Распределение Гаусса,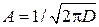

Центральная предельная теорема – при суммировании большого числа независимых случайных величин, имеющих различные распределения, результирующее распределение близко к распределению Гаусса.

Теорема обосновывает применимость нормального распределения к многочисленным случайным процессам. Теорему доказал А. Ляпунов в 1901 г.

Александр Михайлович Ляпунов (1857–1918)

Дата добавления: 2014-02-27; просмотров: 474; Нарушение авторских прав

Мы поможем в написании ваших работ!