Математическое ожидание и дисперсия непрерывных случайных величин

Лекция 8. Числовые характеристики случайных величин. Важнейшие распределения.

Пусть непрерывная случайная величина задана плотностью распределения f(x). Допустим, что все возможные значения .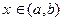

Определение. Мат. ожиданием непрерывной случайной величины X, возможные значения которой принадлежат промежутку (a,b) называется определенный интеграл 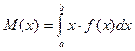(8.1.)

Доказательство: разобьем отрезок (a,b) на n частичных отрезков длиной 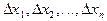. Выберем в каждой из них точку 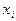(i=1,2, ... ,n).

Определим мат. ожидание непрерывной случайной величины по аналогии с дискретной. Составим сумму произведений возможных значений 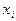на вероятности попадания их в интервал :

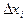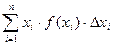
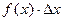приблизительно равно вероятности попадания X в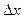

Перейдя к пределу при 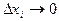, т.е. при стремлении к нулю наибольшего из отрезков, получим: .

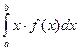Если возможное значение X принадлежат оси OX, то .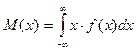

Предполагается, что несобственный интеграл сходится абсолютно, т.е. существует интеграл .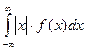

Поаналогии с дисперсией дискретных величин определяется и дисперсия непрерывных величин.

Определение. Дисперсией непрерывных случайных величин называется мат. ожидание квадрата их отклонения.

Если возможные значения 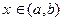, то дисперсия

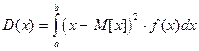. (8.2.)

Если возможное значение принадлежит всей оси, то .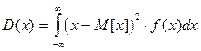

Среднее квадратическое отклонение непрерывной случайной величины определяется как и для величины дискретной .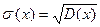

Следствие 1. Вероятность того, что случайная величина примет значение в интервале (a,b) равна приращению функции распределения в этом интервале.

Следствие 2.Вероятность того, что непрерывная случайная величина X примет одно определенное значение, равное 0.

Дата добавления: 2014-02-26; просмотров: 681; Нарушение авторских прав

Мы поможем в написании ваших работ!