
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Плотность распределения вероятности непрерывности случайной величины
Таким образом непрерывную случайную величину, можно также задать используя другую функцию, называющуюся плотностью распределения или плотностью вероятностью или дифференциальной функцией.
Определение: плотность распределения вероятностей непрерывной случайной величины Х называют функцию f(x) - первую производную от функции распределения F(x)
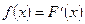
Таким образом функция распределения является первообразной для плотности распределения. Для описания распределения вероятности дискретной случайной величины плотность распределения неприменима.
Вероятность попадания непрерывной случайной величины в заданный интервал.
Теорема 7.1: вероятность того, что непрерывная случайная величина Х примет значение принадлежащую интервалу 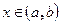 равна определённому интегралу от плотности распределения взятому в пределах от a до b:
равна определённому интегралу от плотности распределения взятому в пределах от a до b:
 (7.1)
(7.1)
Замечание: если f(x) чётная функция и концы интервалов симметричны относительно начала координат то
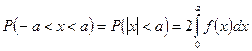
Нахождение функции распределения по известной плотности распределения.
Зная плотность распределения f(x), можно найти функцию распределения по формуле
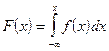
Доказательство: действительно, по определению F(x)=P(X<x), очевидно, что неравенство X<x можно записать в виде 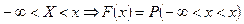 . Полагая, что в соотношении (7.1)
. Полагая, что в соотношении (7.1) 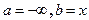 , получим, что
, получим, что
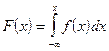 .
.
Таким образом, зная плотность распределения можно записать функцию распределения и наоборот
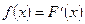
Пример: найти функцию распределения по данной плотности.
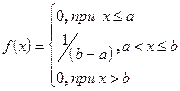
Построить график.
Решение:
если 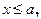 то
то 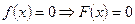 ;
;
если a<x<b, то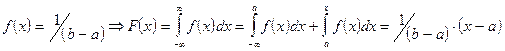 ;
;
если x>b 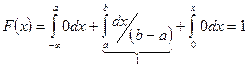 .
.
Функция распределения:
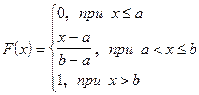
 |




 1
1
 |
a b
Свойства плотности распределения:
- плотность распределения неотрицательная функция.
Доказательство: функция распределения неубывающая функция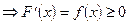 , график плотности распределения называется кривой распределения.
, график плотности распределения называется кривой распределения.
- несобственный интеграл равен 1 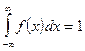 .
.
Доказательство: 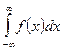 выражает вероятность события состоящая в том, что случайная величина принимает значение принадлежащие интервалу
выражает вероятность события состоящая в том, что случайная величина принимает значение принадлежащие интервалу 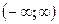 . Очевидно, что такое событие достоверно, следовательно вероятность события равна 1. В частности если возможное значение случайной величины принадлежит отрезку
. Очевидно, что такое событие достоверно, следовательно вероятность события равна 1. В частности если возможное значение случайной величины принадлежит отрезку 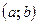 , то
, то 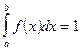
| <== предыдущая страница | | | следующая страница ==> |
| Функция и плотность распределения вероятности непрерывной случайной величины | | | Математическое ожидание и дисперсия непрерывных случайных величин |
Дата добавления: 2014-02-26; просмотров: 1407; Нарушение авторских прав

Мы поможем в написании ваших работ!