Бесконечно большие величины

Функция f(x) называется бесконечно большой величиной при х ® х₀, если для "M > 0 найдется такое d > 0 (d (M)), что для "x ¹ x_0, |х – x₀| < d будет верно: | f(x | > M.

Замечание. Бесконечно большая величина есть функция неограниченная при х ® х₀ (¥). В то же время не всякая неограниченная функция является бесконечно большой. Например, функция y = x sin x является неограниченной, но не бесконечно большой, т.к. с ростом х функция все время колеблется, переходя от положительных к отрицательным значениям и наоборот.

Свойства бесконечно больших величин:

1. Произведение бесконечно большой величины на функцию, предел которой отличен от нуля, есть величина бесконечно большая.

2. Сумма бесконечно большой величины и ограниченной функции есть величина бесконечно большая.

3. Частное от деления бесконечно большой величины на функцию, имеющую предел в точке х₀, есть величина бесконечно большая.

Связь между бесконечно малыми и бесконечно большими величинами устанавливает следующая теорема:

Теорема: Если a(x) есть бесконечно малая при х ® х₀ (¥), то функция f(x) = 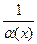является бесконечно большой при х ® х₀ (¥). Обратно, если функция a(x) есть бесконечно большая при х ® х₀ (¥), то функция f(x) = 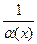есть бесконечно малая при х ® х₀ (¥).

Вопросы для контроля:

1. Что такое предел функции?

2. Что такое предел последовательности?

3. Сколько есть замечательных пределов? Напишите их.

Дата добавления: 2014-02-28; просмотров: 676; Нарушение авторских прав

Мы поможем в написании ваших работ!