Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Практическая значимость дифференциального исчисления
Определение производной функции
Определение дифференциала функции
Лекции 4-6
Производная и ее приложения. Дифференциал функции.
План лекции:
Пусть функция y=f (x) определена на промежутке X и дифференцируема в окрестности точки xЄ X . Тогда существует конечная производная
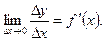
Отсюда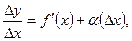 
где a(∆ x) бесконечно малая при ∆x®0, или Dy = f ` (x Dx + a(∆x)∆x.
Таким образом, приращение функции Dy состоит из двух слагаемых – линейного относительно Dx и нелинейного, представляющего бесконечно малую более высокого порядка, чем Dx.
Дифференциаломфункции называется главная, линейная относительно Dx часть приращения функции, равная произведению производной на приращение независимой переменной
Например, дифференциал функции y = x: dy = dx = x`Dx, откуда dx = Dx. Поэтому формулу для дифференциала функции можно записать в виде :
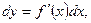откуда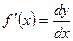 
Геометрический смысл дифференциала: приращение ординаты касательной, проведенной к графику функции y= f (x) в данной точке, когда x получает приращение Dx.
Свойства дифференциала в основном аналогичны свойством производной:
1. 
.
2. 
.
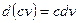3. 
.
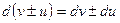4. 
.
5. 
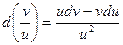
Рассмотрим сложную функцию y = f [j(x)]. Если функции y =f(u) и u= j(x) - дифференцируемые функции своих аргументов, то производная сложной функции равна y’ =f’(u)u’ . Тогда дифференциал функции
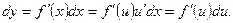
Таким образом,dy=f`(u)du. Это означает, что формула дифференциала не изменяется, если вместо функции от независимой переменнойx рассмотреть функцию от зависимой переменнойu. Это свойство дифференциала называетсяинвариантностьюформы дифференциала.
| <== предыдущая страница | | | следующая страница ==> |
| Бесконечно большие величины | | | Применение дифференциала в приближенных вычислениях |
Дата добавления: 2014-02-28; просмотров: 500; Нарушение авторских прав
Мы поможем в написании ваших работ!