Главная страница Случайная лекция
Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика
Мы поможем в написании ваших работ!
Применение дифференциала в приближенных вычислениях
Поскольку Dy =dy +a (Dx)Dx , приращение функции Dy отличается от её дифференциала на бесконечную малую величину более высокого порядка, чем dy =f`(x)Dx, Поэтому при достаточно малых Dx Dy » dy, или f (x+Dx)-f(x) »f ` (x) Dx,
откуда
f(x + Dx) » f(x) + f ` (x) Dx,
Чем меньше Dx , тем точнее эта формула .
Пример. Вычислить приближенно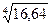 
,
Решение . Приближенная формула для вычисления корней n -й степени :
, поэтому 
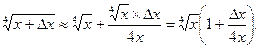
Возьмем x =16; Dx =0,64 ;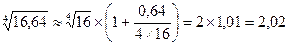
С помощью дифференциала может быть решена задача определена абсолютной и относительной погрешности функции по заданной погрешности измерения аргумента.
Пусть необходимо вычислить значение y =f(x) при некотором x1 , истинная величина которого неизвестна, а известно лишь его приближенное значение x с абсолютной погрешностью ½Dx½=½x –x1½. Если взять вместо истинного значения f(x1) величину f (x) , то ошибка составит
.
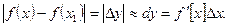Относительную погрешность функции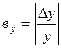 
можно вычислить при малых Dx
по формуле :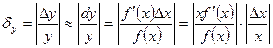 
, или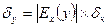 
,где Ex (y) – эластичность функции , δx =
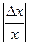- относительная погрешность аргумента x.
Пример. Расход бензина y(л) автомобиля на 100 км пути в зависимости от скорости x(км/ч) описывается функцией y=18 - 0,3x + 0,003x2. Оценить относительную погрешность вычисления расхода бензина при скорости x= 90 км/ч с точности до 5%.
Решение. Найдем эластичность функции по абсолютной величине:
При x =90 бy = 1,41 * 5 » 7,05%.
| <== предыдущая страница | | | следующая страница ==> |
| Практическая значимость дифференциального исчисления | | | Вычисление производных |
Дата добавления: 2014-02-28; просмотров: 880; Нарушение авторских прав
Мы поможем в написании ваших работ!