
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Вычисление производных
Пример 1. Найти производную функцию 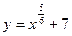 .
.
Пользуясь основными правилами дифференцирования и таблицами производных основных элементарных функций, получаем :
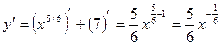 `
`
Пример 2. 
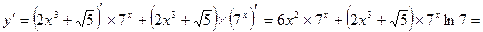

Пример 3. 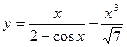
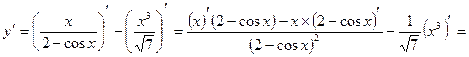
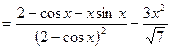
Пример 4. 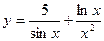
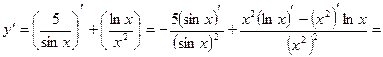

При вычислении производных сложных функций y =f (u) , где u - дифференцируемая функция от некоторой переменной, удобно пользоваться таблицей производных в такой форме:
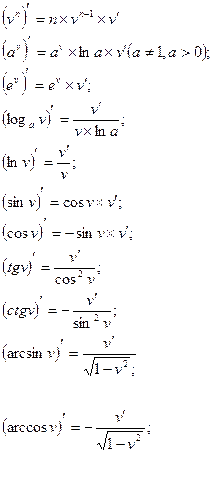 `
`

Пример 5. y= log5 ( x3 –1) , т.е. y= log5 v , где v =x3 –1.
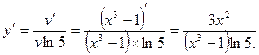
Пример 6. y = cos 5x , т.е. y= cos n , где n =5x.

Пример 7. y = sin3 x, т.е. y= v 3 , где v = sin x.

Пример 8. y = sin x3, т.е. y= sin v , где v = x3 .
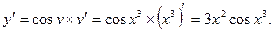
Пример 9. Найти производную от неявной функции x2 +3xy + y2 + 1 =0 и вычислить y` в точке (2; -1).
Дифференцируя по x, получаем :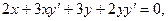 отсюда
отсюда
 . Подставим x =2 , y = -1, получим
. Подставим x =2 , y = -1, получим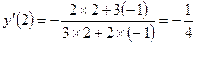
Примерные тесты
| 1. Введение в анализ | ||
| В общей записи функции y=f(x) через у обозначают: | зависимую переменную | |
| независимую переменную | ||
| закон соответствия | ||
| В общей записи функции y=f(x) через х обозначают: | независимую переменную | |
| зависимую переменную | ||
| закон соответствия | ||
| В общей записи функции y=f(x) через f обозначают: | закон соответствия | |
| независимую переменную | ||
| зависимую переменную | ||
| Функция y=f(x) называется четной, если для любого х из области определения: | f(-x)=f(x) | |
| f(-x)=-f(x) | ||
| f(-x)=f(x)+f(-x) | ||
| f(-x)=f(x)-f(-x) | ||
| 2. Дифференциальное исчисление и приложение производной | ||
| Если функция y=f(х) дифференцируема в точке х0, то она в этой точке: | непрерывна | |
| может иметь разрыв 1-го рода | ||
| может иметь разрыв 1-го или 2-го рода | ||
| может быть непрерывной, а может иметь разрыв | ||
| Если функция y=f(х) непрерывна в точке х0, то она в этой точке: | может быть не дифференцируемой | |
| дифференцируема | ||
| не дифференцируема | ||
| Функция называется гладкой на промежутке Х, если она на этом промежутке: | имеет непрерывную производную | |
| имеет производную с конечным числом точек разрыва 1-го рода | ||
| имеет производную с бесконечным числом точек разрыва 1-го рода | ||
| имеет производную с конечным числом точек разрыва 2-го рода | ||
| Функция называется кусочно-гладкой на промежутке Х, если её производная на этом промежутке: | имеет конечное число точек разрыва 1-го рода | |
| имеет конечное число точек разрыва 2-го рода | ||
| имеет бесконечное число точек разрыва 2-го рода | ||
| непрерывна | ||
| 4.Практикум по пределам и производным | ||
Производная функции  равна: равна:
| 
| |

| ||

| ||
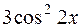
| ||
Производная функции 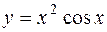 равна: равна:
| 
| |
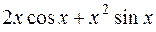
| ||
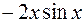
| ||

| ||
Производная функции 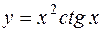 равна: равна:
| 
| |

| ||

| ||

| ||
Приближенное значение  равно: равно:
| 2,0125 | |
| 2,0123 | ||
| 2,0124 | ||
| 2,0126 | ||
Наибольшее значение функции  на отрезке [-2; 2] равно на отрезке [-2; 2] равно
| ||
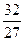
| ||
Значение функции  в точке перегиба равно в точке перегиба равно
| 
| |

| ||
| –2 | ||

| ||
График функции  имеет наклонные асимптоты имеет наклонные асимптоты
| 
| |
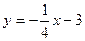
| ||

| ||
| не имеет наклонных асимптот | ||
Предел 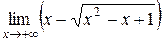 равен: равен:
| 1/2 | |
| 3/2 | ||
Предел  равен: равен:
| 1/2 | |
| 3/2 | ||
Предел последовательности  равен: равен:
| 1/е | |
| е | ||

|
Вопросы для контроля:
1. Запишите основные правила дифференцирования.
2. Как используются производные в экономике.
3. Как производить исследование функции с помощью производных?
| <== предыдущая страница | | | следующая страница ==> |
| Применение дифференциала в приближенных вычислениях | | | Лекция 7-8 |
Дата добавления: 2014-02-28; просмотров: 655; Нарушение авторских прав

Мы поможем в написании ваших работ!