
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция 7-8
План лекции:
1. Первообразная функции и неопределенный интеграл.
2. Свойства неопределенного интеграла.
3. Методы вычисления неопределенного интеграла.
Неопределённый интеграл
Первообразная функция и неопределённый интеграл
Функция F(x) называется первообразной функцией для функции f(x) на промежутке Х, если в каждой точке х этого промежутка F'(х)=f(x).
Например, F(x)=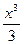 является первообразной для функции f(x)=x2, поскольку
является первообразной для функции f(x)=x2, поскольку 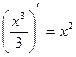 .
.
Теорема. Если F1(x) и F2(x) – первообразные для функции f(x) в некотором промежутке Х, то найдётся такое число С, что
F2(x)=F1(x)+C
Следовательно, если F(x) – первообразная для f(x), то выражение вида F(x)+C, где С – произвольное число, задаёт все возможные первообразные для f(x).
Совокупность всех первообразных для функции f(x) на промежутке Х называется неопределённым интегралом от функции f(x) и обозначается
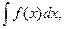
где 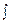 - знак интеграла, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.
- знак интеграла, f(x) – подынтегральная функция, f(x)dx – подынтегральное выражение.
Таким образом,
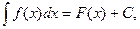
где F(x) – некоторая первообразная для f(x), C – произвольная  постоянная.
постоянная.
Пример: 
Операция нахождения неопределённого интеграла от некоторой функции называется интегрированием этой функции.
Свойства неопределённого интеграла. Интегралы от основных элементарных функций.
Основные свойства неопределённого интеграла:
1. Производная от неопределённого интеграла равна подынтегральной функции, т.е.

2. Дифференциал неопределённого интеграла равен подынтегральному выражению, т.е.

3. Неопределённый интеграл от дифференциала некоторой функции равен этой функции с точностью до постоянного слагаемого, т.е.

где С – произвольное число.
4. Постоянный множитель можно выносить за знак интеграла, т.е.

где  - некоторое число.
- некоторое число.
5. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций, т.е.

Основные табличные интегралы, т.е. интегралы от основных элементарных функций:
 (1)
(1)
 (2)
(2)
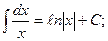 (3)
(3)
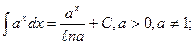 (4)
(4)
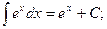 (5)
(5)
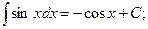 (6)
(6)
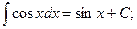 (7)
(7)
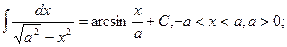 (8)
(8)
 (9)
(9)
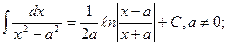 (10)
(10)
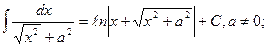 (11)
(11)
Примеры:

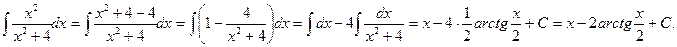
| <== предыдущая страница | | | следующая страница ==> |
| Вычисление производных | | | Интегрирование по частям |
Дата добавления: 2014-02-28; просмотров: 655; Нарушение авторских прав

Мы поможем в написании ваших работ!