Интегрирование по частям

Метод замены переменной

Метод описывается формулой:

где 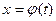- функция, дифференцируемая на рассматриваемом промежутке.

Пример.

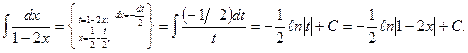
Теорема. Пусть F(x) – некоторая первообразная для функции Тогда

где и - некоторые числа, .

Пример.

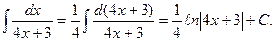
Пусть 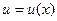- дифференцируемые функции. По свойству дифференциала

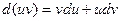, или Интегрируя левую и правую части последнего равенства, получим:

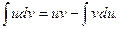
Эта формула называется формулой интегрирования по частям для неопределённого интеграла. Здесь подынтегральное выражение разбивается на два сомножителя - и При этом дифференцирование может существенно упростить один из сомножителей. Если при этом интегрирование не слишком усложнит другой, достигается упрощение процесса интегрирования.

Пример.

В некоторых случаях интегрировать по частям приходится более одного раза.

Пример.

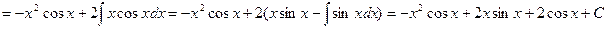
Интегрирование по частям применяется к следующим типам интегралов:

1.

Здесь формулу применяют раз, в первом применении 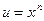, остальные сомножители , пока степень переменной 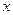не станет равной нулю.

2.

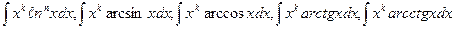
Здесь принимают , остальные сомножители задают выражение для .

Пример.

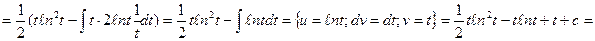
Вопросы для самоконтроля:

1. Как выполняется замена переменной и интегрирование по частям в неопределенном интеграле.

2. Интегрирование простейших рациональных дробей.

Дата добавления: 2014-02-28; просмотров: 569; Нарушение авторских прав

Мы поможем в написании ваших работ!