
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Лекция9
План лекции:
1. Понятие определенного интеграла.
2. Свойства определенного интеграла.
3. Определенный интеграл как функция верхнего предела
4. Вычисление площади плоских фигур.
Определённый интеграл.
Понятие определённого интеграла.
Пусть на 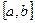 задана функция
задана функция 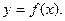 Разобьём отрезок
Разобьём отрезок 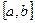 на
на 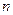 элементарных отрезков точками
элементарных отрезков точками 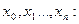
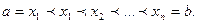 На каждом отрезке
На каждом отрезке 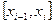 выберем точку
выберем точку 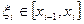 , обозначим
, обозначим  Сумма вида:
Сумма вида:
 (1)
(1)
называется интегральной суммой для функции 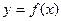 на
на  Геометрический смысл интегральной суммы: сумма площадей под ломаной, образованной на каждом отрезке отрезком прямой
Геометрический смысл интегральной суммы: сумма площадей под ломаной, образованной на каждом отрезке отрезком прямой 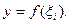
Обозначим через 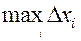 максимальную из длин отрезков
максимальную из длин отрезков 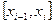 ,
,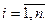
Пусть предел интегральной суммы (1) при  существует, конечен и не зависит от способа выбора точек
существует, конечен и не зависит от способа выбора точек 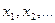
 и точек
и точек  Тогда этот предел называется определённым интегралом от функции
Тогда этот предел называется определённым интегралом от функции 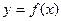 на
на  обозначается
обозначается  , а сама функция
, а сама функция 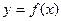 называется интегральной на отрезке
называется интегральной на отрезке  ,т.е.
,т.е.
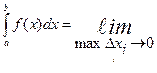
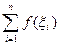
 .
.
Здесь а - нижний предел, b – верхний предел.
Не имеет значения, какой буквой обозначена переменная интегрирования в определённом интеграле:
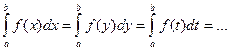 ,
,
поскольку смена обозначений не влияет на поведение интегральной суммы (1).
Отличие определённого интеграла от неопределённого:  представляет собой семейство функций, а
представляет собой семейство функций, а  есть определённое число.
есть определённое число.
В выражении для определённого интеграла предполагается, что a <b. По определению считаем:
 =
=  .
.
Если принять a=b, то интеграл равен нулю.
Геометрический смысл определённого интеграла  в случае a <b, когда функция f(x)
в случае a <b, когда функция f(x)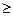 0 на [a,b], состоит в площади под кривой y=f(x) на отрезке [a,b], поскольку при
0 на [a,b], состоит в площади под кривой y=f(x) на отрезке [a,b], поскольку при  ломаная неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
ломаная неограниченно приближается к исходной кривой и площадь под ломаной переходит в площадь под кривой.
Теорема. (достаточное условие существования определённого интеграла). Если функция 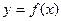 непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
непрерывна на отрезке [a,b], то она интегрируема на этом отрезке.
Свойства определённого интеграла.
1. Постоянный множитель можно выносить за знак интеграла:

2. Интеграл от алгебраической суммы двух функций равен такой же сумме интегралов от этих функций:

3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов по всем частям этого отрезка:

для любых a,b,c.
Геометрический смысл свойства: S=S1+S2, где S1=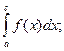 S2=
S2=
4. Если на отрезке [a,b], где a <b, f(x)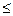 g(x), то
g(x), то
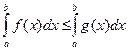
Следствие. Пусть на [a, b], a <b,  , тогда
, тогда 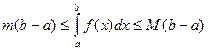 .
.
5. Теорема о среднем. Если функция y=f(x) непрерывна на отрезке [a, b], где a <b, то  :
: 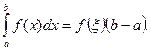
Геометрический смысл теоремы о среднем при 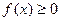 на [a, b] в том, что на отрезке [a, b] найдётся точка
на [a, b] в том, что на отрезке [a, b] найдётся точка  такая, что площадь под кривой f(x) на [a, b], равна площади прямоугольника со сторонами
такая, что площадь под кривой f(x) на [a, b], равна площади прямоугольника со сторонами 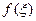 и
и 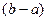 .
.
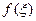
Определённый интеграл как функция верхнего предела.
ξ
Если функция y=f(x) интегрируема на отрезке [a, b], то она интегрируема и на произвольном отрезке [a,x], вложенном в [a, b].
Положим по определению:
 (2)
(2)
где 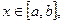 а функция Ф(х) называется интегралом с переменным верхним пределом.
а функция Ф(х) называется интегралом с переменным верхним пределом.
Теорема. Если функция 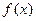 непрерывна на отрезке [a, b], то функция Ф (х) также непрерывна на [a, b].
непрерывна на отрезке [a, b], то функция Ф (х) также непрерывна на [a, b].
Теорема. Пусть 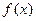 непрерывна на отрезке [a, b], тогда для любого
непрерывна на отрезке [a, b], тогда для любого 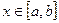 .
.
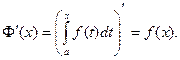
Следствие. Если функция 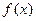 непрерывна на отрезке [a, b], то для этой функции существует первообразная на [a, b].
непрерывна на отрезке [a, b], то для этой функции существует первообразная на [a, b].
Примером первообразной для 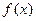 является функция Ф(х), заданная формулой (2).
является функция Ф(х), заданная формулой (2).
| <== предыдущая страница | | | следующая страница ==> |
| Интегрирование по частям | | | Формула Ньютона-Лейбница |
Дата добавления: 2014-02-28; просмотров: 487; Нарушение авторских прав

Мы поможем в написании ваших работ!