Астрономическая, когда наблюдаемый объект находится на бесконечно большом расстоянии, ЭМВ проходят через всю толщу атмосферы и наблюдения выполняют с поверхности Земли

Установить для территории страны высокоточную единую геодезическую систему координат и поддерживать ее на уровне современных и перспективных требований экономики, науки и обороны страны.

Следует заметить, что спутниковые технологии не всегда можно использовать при решении традиционных геодезических задач, например недостаточна относительная точность определений на коротких расстояниях, ограничено использование GPS-методов в точной инженерной геодезии. Сложно использовать GPS в закрытой и полузакрытой местности из-за экранирования спутниковых сигналов, что приводит к необходимости дополнительной привязки объектов обычными методами. Кроме отмеченных имеются и другие недостатки GPS-методов, которые приводят к необходимости наряду со спутниковыми использовать и традиционные технологии выполнения геодезических работ.

ПРЕДВАРИТЕЛЬНАЯ ОЦЕНКА ТОЧНОСТИ ГЕОДЕЗИЧЕСКИХ СЕТЕЙ

Способы оценки точности геодезических построений

Оценку точности геодезической сети выполняют на стадии ее проектирования и после построения и уравнивания сети. Оценка точности на стадии проектирования сети позволяет изучить закономерности действия ошибок измерений при передаче азимутов и длин сторон в различных построениях; установить выгоднейшую форму треугольников в триангуляции и трилатерации; определить частоту размещения базисных сторон и азимутов Лапласа; рассчитать величины продольного и поперечного сдвигов диагоналей ряда геометрических фигур или замыкающих линий ходов, по которым судят о точности передачи координат, и решить ряд других вопросов, связанных с нахождением оптимального варианта построения сети.

В настоящее время точность построения геодезических сетей в основном определяют на ЭВМ по методу наименьших квадратов с учетом всех геометрических и корреляционных связей между уравненными элементами. Для любого уравненного элемента сети

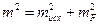, (1)

где m, m_исх – с.к.о. уравненного элемента и исходных данных; m_F – с.к.о. функции F уравненных величин, значение которой определяется по формуле

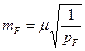, (2)

где μ – с.к.о. единицы веса; 1/p_F – обратный вес функции F.

Формула (2) применяется как на стадии проектирования, так и при окончательном уравнивании сети. Значение 1/p_F в обоих случаях определяется одинаково. Различие заключается в методе определения значений μ. На стадии проектирования ее значение получают из обработки аналогичных сетей, построенных ранее. При уравнивании сети ошибку единицы веса определяют по формуле

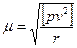, (3)

где v – поправки в непосредственно измеренные с весом р величины, r – число избыточных измерений в сети.

Вес непосредственно измеренной величины в общем случае определяется по формуле

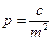. (4)

На стадии проектирования m определяют из аналогичных ранее построенных сетей. Веса запланированных измерений направлений N, азимутов ά и расстояний s вычисляют по формулам

(5)

Учитывая, что горизонтальные направления в данной сети измерены равноточно, целесообразно принять 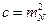. Тогда

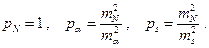(6)

Входящие в формулы (6) m_N , m_ά, m_s целесообразно получать по свободным членам условных уравнений, которые являются результатом совокупного влияния на измеряемые величины случайных и систематических ошибок. В триангуляции для определения т используют формулу Ферреро

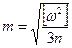, (7)

где ώ – невязка в треугольнике, n – число невязок.

Значение

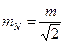. (8)

Для определения т_ά на пунктах Лапласаиспользуют формулу

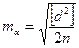, (9)

где d – разности взаимно обратных пунктов, n – число разностей.

В трилатерации и линейно-угловых сетях, используя свободные члены ω_i линейных уравнений центральных систем и геодезических четырехугольников, для определения m_S целесообразно применять формулу

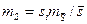, (10)

где

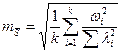. (11)

В формулах (10), (11) s_i – длина i стороны, 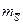- с.к.о. измерения стороны средней длины , k – число свободных членов ω_i , - сумма квадратов коэффициентов условного уравнения i-го геодезического четырехугольника и центральной системы.

В настоящее время широкое применение для априорной оценки геодезических сетей находит метод моделирования результатов измерений. Этот метод позволяет найти точность определения всех элементов построения, однако требует большого объема вычислений, и его целесообразно реализовать на ЭВМ.

Оценка точности триангуляции по приближенным формулам

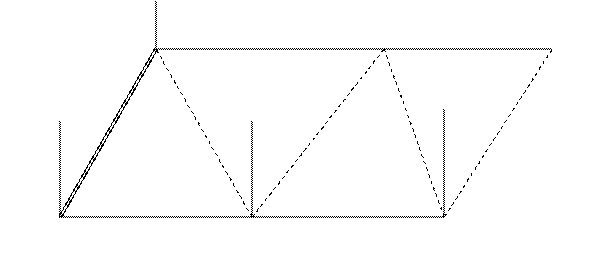
Стороны s – общие для двух соседних треугольников, называют связующими, а противолежащие им углы А и В – связующими углами. Стороны с называют промежуточными, а противолежащие им углы С- промежуточными углами. На рисунке по ходовой линии

(1)

Положим, что ошибки α₀ и углов С_i являются случайными и независимыми. Используя формулу с.к.о. функции 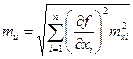, (ч.пр.) при 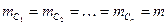для функции (1) находим

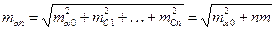. (2)

Если предварительно сделать уравнивание за условие фигур, то

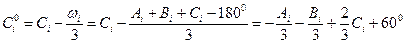. (3)

Полагая в (1) С = С⁰ с учетом (3) имеем

.

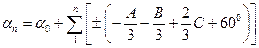По формуле с.к.о. функции получим

.

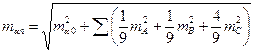При 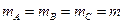имеем

. (4)

Разделив левые и правые части формул (4), (2) и принимая в формуле (4) 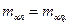при 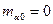, находим

. (5)

Следовательно, предварительное уравнивание ряда триангуляции за условия фигур повышает точность передачи азимута примерно на 18%.

Если азимуты начальной и конечной линий ряда триангуляции известны, то для связующей стороны k, находящейся внутри ряда, 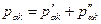, где 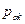- вес азимута стороны k, - веса азимута этой стороны, получаемой от твердой начальной и конечной сторон соответственно. Так как 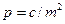, то 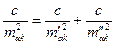, откуда

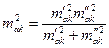, (6)

где

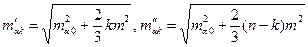. (7)

Наиболее слабой в отношении точности является связующая сторона в середине ряда, т.е. при 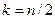. В этом случае ,

,

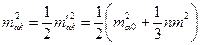а

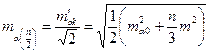. (8)

Если звено триангуляции с известными базисами и азимутами на его концах состоит из равносторонних треугольников и уравнено по направлениям за условия фигур, базисов и азимутов, то

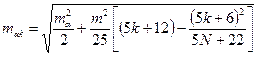, (9)

где N – число треугольников в звене, k – номер треугольника с оцениваемой стороной, m – с.к.о. измерения угла, m_α – с.к.о. определения азимутов.

Средняя квадратическая ошибка передачи связующей стороны в ряде триангуляции

На рисунке по теореме синусов имеем

.

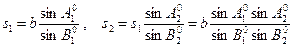Аналогично

.

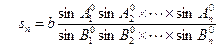Логарифмируя, получим

.

Если предварительно выполнено уравнивание за условие фигур, то

.

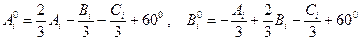С учетом этих значений

.

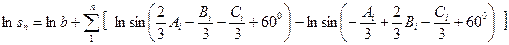Положим, что ошибки измерения b и углов A_i, B_i, C_i являются случайными и независимыми. Применяя формулу с.к.о. функции, при , получим

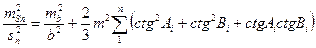. (10)

Величина 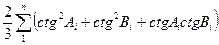не зависит от точности измерений, а зависит только от величин углов A_i, B_i , т.е. от формы треугольника, ее называют ошибкой геометрической связи, или геометрическим весом.

Значение 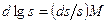, где М = 0,43429 – модуль перехода от десятичного логарифма к натуральному. Переходя к с.к.о., находим 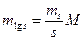, откуда

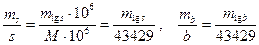. (11)

Используя формулу разложения в ряд Тейлора, имеем

.

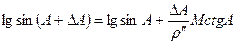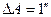Принимая , при получим

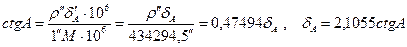, (12)

где - изменение логарифма синуса при изменении угла на 1” (единицы 6-го знака логарифма, деленные на 1”). Аналогично

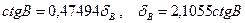. (13)

С учетом (11) – (13) находим

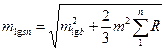, (14)

где .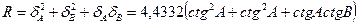

При уравнивании по направлениям, учитывая , где μ – с.к.о. измерения направления, вместо (14) получим

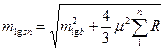. (15)

Если звено триангуляции состоит из равносторонних треугольников с базисами и азимутами на концах звена и уравнено по направлениям за условия фигур, базисов и азимутов, то в таком звене

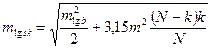, (16)

где N – число треугольников в звене, k – номер треугольника с оцениваемой стороной. Продольный m_L и поперечный m_q сдвиги такого звена определяют по формулам

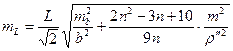, (17)

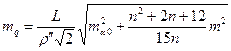, (18)

где n – число промежуточных сторон в диагонали звена . Общий сдвиг

.

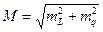Сплошные сети триангуляции

Наиболее распространенными при оценке точности сплошных сетей триангуляции 2 класса являются формулы К.Л. Проворова, который установил, что в сплошной сети триангуляции 2 класса из равносторонних треугольников

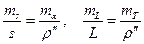, (19)

где m_L, m_T – с.к.о. диагонали L ряда и с.к.о. направления этой диагонали.

Продольный и поперечный сдвиги диагонали ряда равны, т.е.

. (20)

Значение

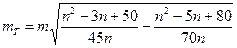, (21)

где m – с.к.о. измерения углов, n – число треугольников в цепочке между конечными пунктами диагонали, N – среднее число треугольников между базисными сторонами в сети. Формула (21) справедлива при n ≤ 5.

В сплошной сети триангуляции, уравненной по углам за все возникающие в ней геометрические условия, с.к.о. дирекционного угла и логарифма стороны определяют по формулам

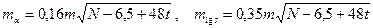, (23)

где

.

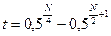В формулах (21) – (23) не учитывают влияние ошибок измерения азимутов и базисных сторон. С учетом этих ошибок

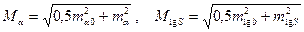, (24)

где m_α , m_lgS – определяют по формулам (23).

Оценка точности трилатерации по приближенным формулам

Средние квадратические ошибки вычисленных углов треугольников

По теореме косинусов

.

Дифференцируя по всем переменным, имеем

,

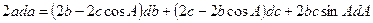откуда, учитывая 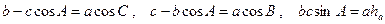, находим

,

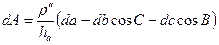где h_а – высота треугольника. Переходя от дифференциалов к с.к.о., имеем

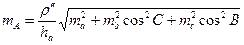. (25)

Аналогично

,

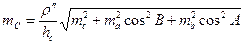. (26)

В равностороннем треугольнике 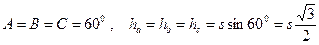; при 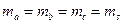, имеем

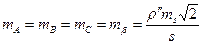. (27)

Из этой формулы, учитывая, что с.к.о. направления 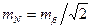, находим

. (28)

Формула (28) устанавливает связь между с.к.о. измерения сторон, углов и направлений.

Продольный и поперечный сдвиги трилатерации

Продольный и поперечный сдвиги трилатерации из равносторонних треугольников с измеренными на его концах азимутами и уравненного за условия азимутов определяют по формулам С.А. Бутлера

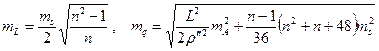, (29)

где n – число треугольников в звене, L – длина диагонали звена, m_s, m_A - с.к.о. измерения длин сторон и азимутов. Общий сдвиг

.

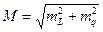Сплошные сети трилатерации из равносторонних треугольников

Исследуя сплошную сеть трилатерации 2 класса размером 200 х 200 км, s = 12,5 км, уравненную за условия азимутов и центральных систем, К.Л. Проворов получил следующие формулы.

С.к.о. относительного положения смежных пунктов

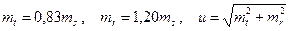, (30)

где m_t, m_r, u – продольный, поперечный и полный сдвиги конца стороны.

С.к.о. относительного положения несмежных пунктов и направления диагонали ряда

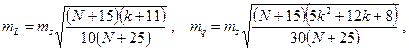
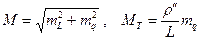, (31)

где L – длина диагонали, соединяющей несмежные пункты, отстоящие друг от друга на k треугольников; N – среднее число треугольников между азимутами Лапласа (k ≤ N), m_s – с.к.о. измерения сторон.

Сделанные расчеты показывают, что в сплошной сети трилатерации поперечный сдвиг диагонали примерно в шесть раз больше продольного. В сплошной сети триангуляции эти сдвиги равны.

Оценка точности линейно-угловых сетей и звеньев полигонометрии.

Согласование точности угловых и линейных измерений в геодезических сетях

ЧАСТОТА РАЗМЕЩЕНИЯ АЗИМУТОВ И БАЗИСНЫХ СТОРОН.

ВЫГОДНЕЙШАЯ ФОРМА ТРЕУГОЛЬНИКОВ

Частота размещения азимутов. Азимуты Лапласа играют важ­ную роль при создании опорных геодезических сетей: обеспе­чивают независимую азимутальную ориентировку сторон гео­дезической сети во всех ее частях, причем с одинаковой высо­кой точностью; позволяют контролировать результаты угловых измерений по невязкам азимутальных условий, ослабляя при этом влияние систематических ошибок измерений; приводят к возникновению азимутальных условных уравнений при уравнивании сети и тем самым способствуют повышению ее точности.

Рассчитаем предельно допустимое число треугольников п_тах, через которое необходимо размещать азимуты Лапласа в три­ангуляции, чтобы они могли выполнять функцию контроля уг­ловых измерений.

Пусть на концах цепочки треугольников изме­рены азимуты α₁ и а₂. Используя промежуточные углы C_i тре­угольников, напишем в общем случае

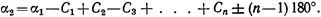
Перейдя к средним квадратическим ошибкам, получим

2т²_α= п т²,

где т_а и т - средние квадратические ошибки измерения ази­мутов и углов соответственно; n - число промежуточных углов, равное числу треугольников между азимутами.

Пусть заданы предельные значения ошибок: т_{а пред} = tm_a и n _пред. = п_тах. Тогда при заданном значении средней квадратической ошибки т" измерения углов и t=2,5, как это принято в геодезии при расчете допусков, найдем

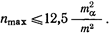
При т_а. =т получим n_mах=12; при т_а. = 1,0"и m = 0,7" - n_mах= 25.

Звенья триангуляции 1 класса состоят из 12-16 треуголь­ников. В сетях триангуляции 2 класса в соответствии с требо­ваниями инструкции азимуты должны определяться не более чем через 25 треугольников.

Частота размещения базисных сторон.Базисные стороны в триангуляции, как и азимуты Лапласа, играют важную роль. Они устанавливают единый масштаб построения геодезических сетей на земной поверхности; позволяют контролировать точ­ность передачи длин сторон, ослабляя при этом накопление си­стематических ошибок измерений; приводят к возникновению базисных условных уравнений при уравнивании геодезической сети и тем самым способствуют повышению ее точности.

В целях обеспечения стройной системы построения государ­ственной геодезической сети азимуты Лапласа принято опреде­лять на обоих концах базисных сторон. Поэтому в триангуля­ции частота размещения базисных сторон такая же, как азиму­тов Лапласа.

Выгоднейшая форма треугольников.В триангуляции любая сторона треугольника имеет одинаково важное значение, поэ­тому связующие S и промежуточные С стороны треугольников должны при прочих равных условиях определяться с одинако­вой высокой точностью. Это требование может быть записано в виде равенства

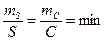
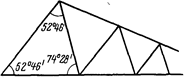
При реализации данного требования треугольники в рядах триангуляции получаются равнобедренными с углами С=А =52°46' и В=74⁰28' . Однако такая форма треугольников не пригодна для практики, поскольку в этом случае ряд «вырож­дается» по мере удаления от исходной базисной стороны. С практической точки зрения наиболее выгодными по форме являются равносторонние треугольники, построение ко­торых, однако, не всегда возможно вследствие особенностей рельефа местности. В рядах триангуляции 1 класса углы в тре­угольниках должны быть не менее 40°, а в сплошных сетях триангуляции 2 класса - не менее 30°.

с

. Схема цепи треугольников с «выгоднейшими» углами

А

в

УГЛОВЫЕ ИЗМЕРЕНИЯ

Классификация угломерных приборов

Теодолиты классифицируют по разным признакам: области применения, физической природе носителя информации, конструкции отсчетного устройства, точности.

По области применения можно выделить следующие группы теодолитов: геодезические (применяемые исключительно для измерения углов в геодезической практике); астрономические (для определения астрономических координат – широты, долготы и азимута); маркшейдерские (для измерений в подземных горных выработках); гироскопические (для определения азимута гироскопическим методом); буссольные (для определения магнитных азимутов направлений при помощи теодолита, рабочей мерой которого служит буссоль); автоколлимационные (для наблюдений методом автоколлимации).

По физической природе носителей информации различают теодолиты механические, оптические, электронные. В механических теодолитах рабочей мерой является металлический лимб, отсчитывание по которому производят при помощи простейших отсчетных устройств (винтового микрометра, верньера, лупы с индексом). У оптических теодолитов лимб изготовлен из оптического стекла, отсчеты по лимбу берут при помощи оптической отсчетной системы со шкаловым микроскопом, микроскопом с индексом или оптическим микрометром. У электронных теодолитов рабочая мера может задаваться электротехническими элементами (индуктивностью, емкостью, резисторами и т.п.) либо датчиками типа «угол – код – цифра». Считывание информации может выполняться визуально с цифрового табло или в автоматическом режиме – с регистрацией на носитель информации.

По конструкции отсчетного устройства теодолиты делят на простые, повторительные, с уровнем при вертикальном круге, с компенсатором и др.

По конструкции оптической системы зрительной трубы различают теодолиты с прямым (земным) изображением и обратным (астрономическим) изображением.

По точности теодолиты делятся на высокоточные, точные и технические. Высокоточные теодолиты позволяют в лабораторных условиях измерять угол одним приемом со с.к.о. 1”, точные – от 1 до 10”, технические – более 10”. Иногда в группе точных теодолитов выделяют две подгруппы: повышенной точности – с погрешностями от 1,5 до 3” и средней точности – от 3 до 10”. Согласно ГОСТу 10529-96 теодолиты обозначают буквой «Т» и числом, соответствующим с.к.о. измерения угла одним приемом в лабораторных условиях: Т05, Т1, Т2 (Т2А), Т5 (Т5К), Т15К, Т30, Т60, 2Т2, 2Т5, 2Т5К, 3Т2КП, 3Т2КА, 3Т5КП. Буква А обозначает теодолит с автоколлимационным окуляром, М – маркшейдерские, Э – электронные, К – с компенсатором, П – труба имеет прямое изображение. Цифрами 2 и 3 перед «Т» обозначают унифицированные теодолиты группы 2Т и 3Т.

Теодолиты Т05, Т1, Т2 имеют двустороннее (по диаметрально противоположным штрихам) отсчитывание по лимбу, а теодолиты Т5, Т15, Т30, Т60 – одностороннее. Все теодолиты, кроме Т60, имеют электроосвещение. В Т1, Т2, Т5 и Т15 оптические центриры встроены в алидаду, в Т30 и Т60 возможно оптическое центрирование через полую вертикальную ось при помощи зрительной трубы.

Разработка теодолитов серии 3Т выполнена с учетом оптимизации оптических и кинематических схем при условии максимальной унификации конструкции узлов и деталей. В серии 3Т использован модульный принцип, при котором конструкция распадается на несколько отдельных модулей (зрительная труба, вертикальная ось с горизонтальным кругом, отсчетная система вертикального круга, микрометр, колонна с горизонтальной осью), которые можно собирать, юстировать, заменять раздельно.

На рисунке изображены основные плоскости и оси теодолита. ГГ, ВВ – следы плоскостей горизонтального и вертикального кругов, LL, ll, l’l’ – ось цилиндрического накладного уровня, цилиндрического уровня при алидаде горизонтального и вертикального кругов; vv, hh, pp – вертикальная ось теодолита, ось вращения зрительной трубы и оси вращения подъемных винтов соответственно; zz – визирная ось, проходит через перекрестие сетки нитей и оптический центр объектива.

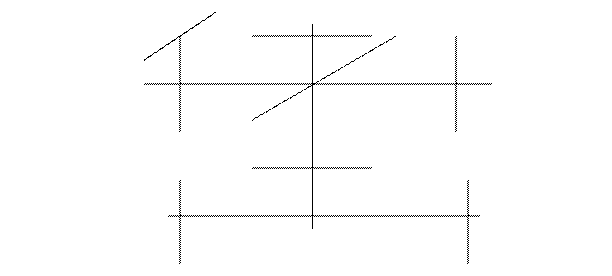
Плоскость горизонтального круга и ось вращения трубы должны быть перпендикулярны вертикальной оси теодолита. Визирная ось трубы должна быть перпендикулярна оси вращения трубы. Ось вращения алидады и ось вращения горизонтального круга должны проходить через центр кольца делений лимба. При угловых измерениях вертикальная ось теодолита должна совпадать с отвесной линией в точке его стояния. Нарушения геометрической схемы теодолита приводят к ошибкам в отсчетах и в итоге – к ошибкам в конечных результатах угловых измерений.

В теодолите должны быть согласованы точность изготовления осевой системы, точность нанесения делений, точность визирования, точность изготовления и компоновки узлов отсчетного устройства, точность изготовления цилиндрических уровней, компенсаторов и т.п.

Высокоточные теодолиты

Высокоточные теодолиты используют при построении государственных геодезических сетей 1, 2, 3 классов, выполнении инженерно-геодезических работ особо высокой точности, при решении научных задач и т.п.

Современными высокоточными теодолитами являются Т05 и Т1 (Россия), Theo-003 (Германия), Т3, Т4 «Вильд» (Швейцария), КМ-3 «Керн» (Швейцария) и др.

Теодолит Т05 выпускается с 1969 г., состоит из двух частей. Верхняя часть содержит зрительную трубу, горизонтальную ось и вертикальный круг; нижняя – подставку с подъемными винтами, горизонтальный круг, вертикальную осевую систему, алидаду с колонками, имеющими лагеры, оптическую систему горизонтального круга. При перевозке или длительном хранении обе части можно разъединить и поместить в разные упаковочные ящики. Зрительная труба – центральная прямая астрономическая с увеличением 62, 50, 37^Х, имеет окулярный микрометр с ценой деления 1”. Окулярные микрометры, состоящие из подвижного биссектора сетки нитей, связанного с отсчетной шкалой микрометра, применяют для уменьшения влияния случайных ошибок визирования. При наблюдении биссектор не менее трех раз наводят на визирную цель и в результате определяют среднее значение ε смещения визирной цели относительно нульпункта биссектора. Выразив ε в угловой мере, определяют поправку в отсчет по лимбу. Применение окулярного микрометра в 1,5-2 раза уменьшает влияние случайных ошибок визирования. С.к.о. измерений одним приемом – 0,5-0,7”. Горизонтальный круг может перемещаться для установки нужного отсчета. Отсчетная система основана на совмещении противоположных штрихов лимба с помощью микрометра с оптическими клиньями. Наименьшее деление кругов – 10’. Теодолит имеет три уровня: накладной с ценой деления τ = 4”, цилиндрический при алидаде горизонтального круга с τ = 6-7”, цилиндрический контактный при алидаде вертикального круга с τ = 10-12”. По заказу потребителя Т05 оснащают поверительной трубой с окулярным микрометром для учета кручения сигнала. Она крепится в подставке теодолита. Перед началом угловых измерений поверительную трубу наводят на расположенную в 1-2 км от пункта визирную цель и закрепительным устройством жестко скрепляют с подставкой теодолита. По разностям отсчетов по поверительной трубе вычисляют поправки в измеренные направления и углы за кручение сигнала. Если кручение не более 1” за 4-5 минут, то поверительную трубу не применяют.

Теодолит Т1изготавливают серийно с 1976 г., он снабжен окулярным микрометром с ценой деления 1” для точного визирования на цель, изображение шкалы микрометра передается в поле зрения трубы. С.к.о. измерений одним приемом – 1,0-1,3” Теодолит имеет три уровня: накладной с ценой деления τ = 5”, цилиндрический при алидаде горизонтального круга с τ = 7”, и при алидаде вертикального круга с τ = 12”. Зрительная труба прямая центральная астрономическая с увеличением 30 и 40^Х, переводится через зенит окулярной частью. На базе Т1 выпускают модификации прибора Т1А с автоколлимационной зрительной трубой.

Угломерный комплект УВКпредназначен для измерения горизонтальных углов и зенитных расстояний в триангуляции и полигонометрии 2 класса, а также в прикладной геодезии. Комплект выпускается в двух вариантах: УВК.Т – для угловых измерений в геодезических сетях, УВК.И – для прикладной геодезии. Угломерная часть комплекта построена на основе хорошо известного теодолита ОТ-02М. Основные конструктивные особенности и принципы работы ОТ-02М сохранены в УВК. Цена деления шкалы оптического микрометра – 0,5”. С.к.о. измерений одним приемом – 1,0-1,5” Цилиндрический уровень при алидаде горизонтального круга с τ = 6-8”, и при алидаде вертикального круга с τ = 10-12”. Увеличение зрительной трубы – 30 и 40^Х.

В новых высокоточных теодолитах используется система отсчета с оптико-электронным сканированием, позволяющая автоматизировать процесс угловых измерений и повысить приборную точность. К таким приборам относится теодолит Т2000S фирмы «Вильд» (Швейцария). Зрительная труба в этом теодолите имеет прямое изображение и увеличение 26, 35, 43, 59^Х. Имеются два режима работы: простой – для высокоточных угловых измерений, и следящий – для наблюдений за подвижной целью. Точность отсчета по кругам 1 или 0,1” – по усмотрению наблюдателя. Теодолит имеет дисплейную панель управления и регистратор.

Поверки и исследования высокоточных теодолитов

Поверки позволяют выявить отклонения в приборе от геометрических условий и оптико-механических требований, юстировкой наиболее полно устраняют эти отклонения.

Исследования определяют постоянные прибора, неустранимые отклонения для введения в результаты измерений соответствующих поправок, правильность работы отдельных узлов теодолита, ошибки диаметров лимба и т.п. По результатам исследований выявляют пригодность теодолита для выполнения измерений данного класса точности.

Обязательными поверками на каждом пункте перед наблюдениями являются следующие.

1. Подъемные и наводящие винты должны вращаться плавно.

2. Вращение алидады должно быть плавным.

3. Ось накладного уровня и ось вращения трубы должны находиться в одной плоскости и быть параллельными. Устанавливают уровень по направлению двух подъемных винтов теодолита и, вращая их, приводят пузырек уровня в нульпункт. Затем уровень поворачивают в обе стороны на горизонтальной оси трубы. Если пузырек не смещается, то первая часть условия выполнена. В противном случае уровень исправляют боковыми юстировочными винтами при нем. Для выполнения второй части поверки пузырек уровня приводят в нульпункт, затем переставляют уровень на оси трубы на 180⁰. На половину дуги отклонения пузырек уровня возвращают в середину вертикальными юстировочными винтами уровня, на вторую половину – подъемными винтами теодолита.У теодолита без накладного уровня ось цилиндрического уровня при алидаде горизонтального круга должна быть перпендикулярна к вертикальной оси вращения теодолита. Поверка и юстировка выполняются аналогично второй части поверки накладного уровня.

4. Ось вращения трубы должна быть перпендикулярна к вертикальной оси вращения теодолита. Вращением алидады устанавливают накладной уровень по направлению двух подъемных винтов, вращая их, приводят пузырек уровня в нульпункт. Затем уровень приподнимают, алидаду поворачивают точно на 180⁰ и уровень опускают на ось трубы. Если пузырек остается в нульпункте, то поверка выполнена. В противном случае на половину дуги отклонения пузырек перемещают к нульпункту регулировочным винтом при лагерах оси вращения трубы, а на вторую половину – подъемными винтами.

5. Наклоны трубы теодолита с помощью наводящего винта не должны приводить к азимутальным смещениям оси трубы в лагерах. Вертикальную нить сетки наводят на нитяной отвес. Если изменение наклона трубы от 87⁰ до 93⁰ не вызывает смещение визирной оси с нити отвеса, то пользоваться наводящим винтом трубы не следует до устранения отмеченного недостатка. Трубу теодолита в этом случае поворачивают рукой.

6. Отсчетное устройство должно быть выверено и отъюстировано: 1) индекс оптического микрометра при установке шкалы на ноль должен совпадать с совмещенным изображением диаметрально противоположных штрихов лимба; 2) освещенность поля зрения отсчетного микроскопа должна быть равномерной; 3) линия раздела между верхним и нижним изображением штрихов лимба должна быть тонкой, прямой, без заметных утолщений; 4) изображения штрихов лимба и шкалы должны быть видны одновременно и резко без изменения фокусировки.

7. Визирная ось трубы должна быть перпендикулярна оси вращения трубы. Возникающая вследствие невыполнения этого условия коллимационная ошибка с = (Л-П) / 2 sin z не должна превышать 10”. Исправление выполняют перемещением сетки нитей на визирную цель после установки на горизонтальном круге отсчета N = (Л+П±180⁰) / 2, свободного от влияния коллимационной ошибки.

8. Нити биссектора окулярного микрометра должны быть вертикальными. Биссектор тщательно отъюстированного теодолита наводят на удаленную точку и вращают зрительную трубу рукой, при этом наблюдаемая точка не должна иметь азимутальное смещение. В противном случае сетку поворачивают юстировочными винтами.

9. Место зенита (MZ), или место нуля (МО), вертикального круга не должно превышать 10”. Местом зенита (местом нуля) называют отсчет по вертикальному кругу при вертикальном (горизонтальном) положении визирной оси трубы и положении пузырька при алидаде вертикального круга в нульпункте. MZ и зенитное расстояние z вычисляют по формулам: для теодолитов ОТ-02М (УВК)

MZ = Л + П – 180⁰ , z = П – Л + 90⁰ ;

для теодолитов Т1

MZ = (Л + П – 360⁰) / 2 , z = Л – MZ ;

для теодолитов Т05 определяют место нуля и угол наклона

МО = (Л + П ± 180⁰) / 2 , ν = Л – МО.

Место зенита (место нуля) приводят к нулю юстировочным винтом уровня при алидаде вертикального круга путем приведения пузырька уровня в нульпункт после установки на вертикальном круге с помощью винта уровня значения z или ν , при этом перекрестие сетки нитей должно быть на точке, при наблюдении которой определяли MZ (МО). Кроме того, исправление MZ (МО) можно сделать так: на вертикальном круге устанавливают MZ (МО), при этом пузырек уровня должен быть в нульпункте; затем винтом уровня устанавливают отсчет, равный нулю. При этом пузырек уровня уйдет с нульпункта, его приводят в нульпункт исправительными винтами уровня.

Высокоточный теодолит после получения его с завода или капитального ремонта тщательно исследуют по полной программе: определяют цену деления уровня накладного и при алидаде; цену деления окулярного микрометра основной и поверительной труб; правильность хода фокусирующей линзы трубы; ошибки совмещения изображений штрихов лимба; рен оптического микрометра; мертвый ход микрометра с плоскопараллельными пластинами; ошибки делений шкалы микрометра; эксцентриситет лимба и алидады; правильность вращения алидады; ошибки деления лимба; средние квадратические ошибки измерения горизонтальных и вертикальных углов в лабораторных условиях одним приемом по отклонениям от среднего из 12 приемов.

Определение рена оптического микрометра

Реном оптического микрометра называют разность между номинальной и измеренной микрометром величинами полуделения лимба. Рен определяют отдельно для микроскопов горизонтального и вертикального кругов, для верхнего и нижнего изображений делений лимба в поле зрения микрометра.

Рен отсчетной системы горизонтального круга определяют при перестановке алидады через 45⁰ + I , где i – цена деления лимба. Прямой ход начинают с отсчета 0⁰00”, обратный – [360⁰ – (22⁰ + i )]. Рен отсчетной системы вертикального круга определяют с перестановкой алидады через 2⁰10’ в интервале от 350⁰ до 4⁰10’ (прямой ход) и от 7⁰50’ до 353⁰40’ (обратный ход) – для теодолита Т05; для теодолитов Т1, ОТ-02М в интервалах от 80⁰00’ до 94⁰10’ (прямой ход) и от 97⁰50’ до 83⁰40’ – обратный ход.

Порядок измерений: на шкале оптического микрометра устанавливают отсчет, близкий к нулю; вращением наводящего винта совмещают диаметрально противоположные штрихи А и А + 180⁰. После этого подготовительного этапа с помощью окулярного микрометра точно совмещают (по два раза) изображения штрихов лимба и берут отсчеты: а – при совмещении штрихов А и А + 180⁰; b – при совмещении А - i и А + 180⁰; с – при совмещении А и А + 180⁰ – i. Рен определяют по формулам

,

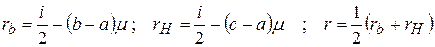где μ – цена деления шкалы микрометра.

Значения r и Δr = r_b – r_H в высокоточных теодолитах не должны превышать 0,5”. При больших значениях нужно отъюстировать отсчетную систему или в измеренные на пункте горизонтальные направления и зенитные расстояния ввести поправки

,

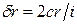где отсчет по микрометру с и цену деления лимба i – выражают в угловых минутах.

Определение эксцентриситета алидады и лимба

Эксцентриситетом алидады называют несовпадение проекции О оси вращения алидады на лимб с центром К кольца делений лимба.

Эксцентриситетом лимба называют несовпадение оси вращения О₁ лимба с центром К кольца делений на нем.

Определение эксцентриситета алидады.На рисунке j – отсчетный индекс оптического микрометра; d – угол смещения индекса относительно расчетного положения; e, Р – элементы эксцентриситета.

Перед исследованием эксцентриситета алидады тщательно выверяют накладной уровень и при его отсутствии – уровень при алидаде и приводят вертикальную ось в отвесное положение. Исследование выполняют при двух полных оборотах алидады по часовой стрелке (прямой ход) и двух полных оборотах против часовой стрелки (обратный ход). Алидаду переставляют через 30⁰. На каждой установке делают два отсчета: t – при совмещении изображений диаметрально противоположных штрихов и t’ – при совмещении ближайшего штриха с отсчетным индексом j микрометра. Кроме того, фиксируют отсчеты по обоим концам пузырька уровня.

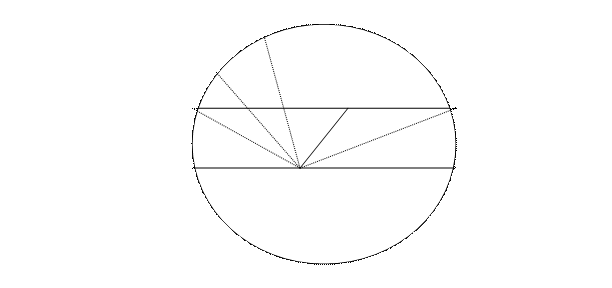
На рисунке 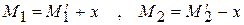, поэтому

Вычитая из второго выражения первое и учитывая, что v = t’ – t имеет случайную ошибку δ, находим

,

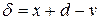где x и d – независимые, v – свободный член.

В треугольнике ОКМ по теореме синусов находим

,

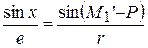откуда, принимая угловой эксцентриситет алидады ,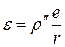

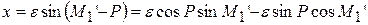
Принимая 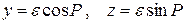, с учетом значения х имеем

.

Свободные члены v находят как среднее из четырех их значений, получаемых для установок M’₁ в двух прямых и двух обратных ходах, что практически исключает из v ошибки вследствие колебания оси вращения алидады. Число уравнений равно числу n установок алидады по всей окружности.

Переходя к нормальным уравнениям, после преобразований находим

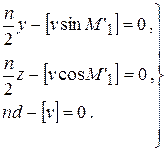
откуда

.

Используя полученные значения y и z , имеем

.

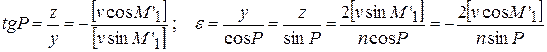Определив ε , находят линейный элемент 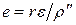. Используя ε , Р и d, вычисляют для всех установок М₁ значения

.

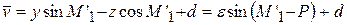По разности 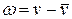, где , т.е. по отклонениям v от синусоиды , судят о правильности вращения алидады вокруг ее оси. По требованиям инструкции колебание v = t’ – t не должно превышать 40” , а 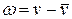- не более 10”, т.е. 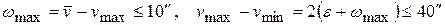, отсюда угловой эксцентриситет алидады .

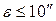Правильность вращения алидады дополнительно можно исследовать по измерениям показаний накладного уровня (уровня при алидаде) при двух ее оборотах в прямом и обратном направлениях.

Определение эксцентриситета лимба.При закрепленной алидаде лимб переставляют через 30⁰, выполняя полный оборот в прямом и обратном ходах. На каждой установке берут отсчеты t - при совмещении диаметрально противоположных штрихов и t’ – при совмещении штриха лимба с индексом. Вычисляют v = t’ – t , затем наносят на график, на котором строят синусоиду, лучшим образом аппроксимирующую экспериментальное построение, и проводят ось симметрии. Угловой эксцентриситет ε₁ равен наибольшей ординате синусоиды, угол Р₁ – углу М в точке пересечения синусоиды с осью симметрии, а d равно ординате оси симметрии. Угловой эксцентриситет ε₁ не должен превышать 10”, а ε + ε₁ < 20”, где ε – угловой эксцентриситет алидады.

Определение ошибок делений и диаметров лимба

Деления на лимбе наносят автоматической делительной машиной со скоростью 3 – 4 деления в минуту. Из-за неточностей изготовления эталонных шестерен машины, погрешностей ее наладки, колебания оси вращения резца, неперпендикулярности лимба к оси вращения, изменения температуры и других причин фактическое положение штриха φ отличается от расчетного на величину δ_φ. При угловых измерениях отсчеты берут по диаметрально противоположным штрихам, т.е. используют диаметр лимба. Поэтому исследуют среднее арифметическое из ошибок штрихов φ и φ + 180⁰, называемое ошибкой х_φ диаметра φ , т.е.

.

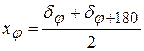Полная ошибка х_φ состоит из систематической х_σ и случайной х_η составляющих:

.

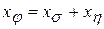Из исследований определяют х_φ и х_σ , а случайные ошибки определяют из разности .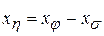

Ошибки диаметров делят на длиннопериодические, изменяющиеся по всему лимбу, и короткопериодические, которые изменяются внутри каждого градуса. В современных высокоточных теодолитах допускают х_φ до 1 – 1,2”.

Так как диаметров лимбов слишком много (при цене деления 10’ их 1080), то определяют ошибки не всех диаметров, а кратных, например, 1 или 3⁰. В каждом способе по определенной программе последовательно измеряют три контрольных угла β₁ , β₂ и β₃, при чем каждый угол β должен укладываться целое число раз в 180⁰ и быть кратным интервалу 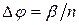, через который будут определяться ошибки диаметров ( в настоящее время принимают β₁ = 36, β₂ = 45, β₃ = 60, Δφ = 3⁰).

Контрольные углы обычно задают двумя коллиматорами, при этом требуется сохранение их постоянства с точностью до 0,01” в течение всего периода измерений по заданной программе. Наиболее простой способ вычисления поправок диаметров лимба предложен С.В. Елисеевым. Поправки определяют со средней квадратической ошибкой порядка 0,1”.

Способы угловых измерений

Результаты угловых измерений в ГГС должны быть равноточными, т.е. на всех пунктах иметь один и тот же вес, и получены с наивысшей точностью при наименьших затратах труда и времени. Для этого высокоточные измерения каждого направления и угла выполняют по строго одинаковой наиболее совершенной методике в периоды наивыгоднейшего времени наблюдений, когда влияние внешней среды минимально. Необходимо, чтобы каждое направление измерялось на разных диаметрах лимба, равномерно распределенных по кольцу делений; в приеме должно быть обеспечено единообразие операций при измерении каждого направления и симметрия во времени относительно среднего для приема времени наблюдений; целесообразно все направления и углы на пункте измерять симметрично относительно момента изотермии воздуха.

Перед выполнением наблюдений на пункте производят осмотр геодезического знака, откапывают центр до марки с меткой, на площадку наблюдателя поднимают теодолит и другое снаряжение, крышу сигнала накрывают брезентом. В результате осмотра наблюдатель должен убедиться в прочности и устойчивости столика сигнала и в том, что внутренняя пирамида не соприкасается с полом площадки для наблюдателя и с лестницей. Обнаруженные недостатки необходимо устранить.

Перед наблюдением с помощью теодолита согласно схеме геодезической сети отыскивают все подлежащие наблюдению пункты и после наведения на них делают с точностью до 1’ отсчеты по горизонтальному и вертикальному кругам. Кроме того, при наведении на пункты положение алидады фиксируют на нижней части прибора с помощью штрихов против индекса на алидаде. Теодолит устанавливают на штатив или столик сигнала не менее чем за 40 минут до начала наблюдений. К измерению горизонтальных направлений приступают при хорошей видимости, когда изображения визирных целей спокойны или слегка колеблются (в пределах 2”).

Измерение отдельного угла.Незакрепленную алидаду отводят влево на 30 – 40⁰ и обратным вращением наводят на визирную цель первого направления так, чтобы она оказалась справа от биссектора, алидаду закрепляют. Наводящим винтом алидады, только ввинчиванием, биссектор наводят на визирную цель и берут отсчет по оптическому микрометру (если имеется окулярный микрометр, то трижды наводят его биссектор на визирную цель и берут отсчеты). Открепляют алидаду и наводят на 2-е направление так же, как и на 1-е. На этом заканчивается полуприем.

Трубу переводят через зенит, по часовой стрелке наводят на 2-е направление, предварительно отведя алидаду на 30 – 40⁰; наводящим винтом биссектор наводят на визирную цель и берут отсчет по оптическому микрометру. По часовой стрелке алидаду поворачивают на угол, дополняющий измеряемый до 360⁰, наводят на визирную цель 1-го направления, берут отчет. Заканчивается прием.

Способ круговых приемов – способ Струве.Способ был предложен в 1816 г. В.Я. Струве, получил широкое применение почти во всех странах. В нашей стране используется в геодезических сетях 2 - 4 классов и сетях более низкой точности.

В этом способе при неподвижном лимбе алидаду вращают по ходу часовой стрелки и биссектор сетки нитей трубы последовательно наводят на первый, второй,…, последний и снова на первый (замыкание горизонта) наблюдаемые пункты, каждый раз отсчитывая по горизонтальному кругу. В этом состоит первый полуприем. Затем трубу переводят через зенит и, вращая алидаду против часовой стрелки, наводят биссектор на те же пункты, но в обратной последовательности: на первый, последний, …, второй, первый; заканчивают второй полуприем и первый прием., состоящий из первого и второго полуприемов.

Между приемами лимб переставляется на угол

,

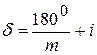где m – число приемов, i – цена деления лимба.

Наведение биссектора на на визирную цель выполняют только ввинчиванием наводящего винта алидады. Перед каждым полуприемом алидаду вращают по ее движению в данном полуприеме.

В результаты измеренных направлений вводят поправки за рен, наклон вертикальной оси теодолита (при углах наклона визирного луча в 1⁰ и более) и поправки за кручение знака – по отсчетам по окулярному микрометру поверительной трубы.

Контроль угловых измерений: по расхождениям значений первого направления в начале и конце полуприема (незамыкание горизонта), по колебанию двойной коллимационной ошибке, определяемой для каждого направления, и по расхождению приведенных к нулю значений одноименных направлений, полученных в разных приемах. В триангуляции 2 – 4 классов незамыкание горизонта и колебание направлений в приемах не должны превышать 5, 6 и 8” для Т05, Т1; ОТ-02 и Т2; колебание 2С – 6,8 и 12” для этих же теодолитов соответственно.

В пунктах 2 класса направления измеряют 12-15 круговыми приемами, на пунктах 3 класса – 9, на пунктах 4 класса – 6, а в сетях полигонометрии 2, 3, 4 классов – 18, 12, 9 приемами.

Уравнивание на станции сводится к вычислению среднего значения по каждому направлению из m приемов. При этом предварительно все измеренные направления приводят к начальному, придав ему значение 0⁰00’00,00”. Вес уравненного направления равен p = m – числу приемов измерений. Для оценки точности направления обычно применяют приближенную формулу Петерса

,

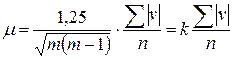где μ – с.к.о. направления, полученного из одного приема (с.к.о. единицы веса); ∑‌‌[v] – сумма абсолютных величин уклонений измеренных направлений от их средних значений, вычисленных по всем направлениям; n, m – число направлений и приемов соответственно. Значения k при m = 6, 9, 12, 15 равны 0,23; 0,15; 0,11; 0,08. С.к.о. уравненного направления (среднего из m приемов) вычисляют по формуле

.

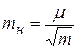Достоинстваспособа круговых приемов: простота программы измерений на станции; значительное ослабление систематических ошибок делений лимба; высокая эффективность при хорошей видимости по всем направлениям.

Недостатки:сравнительно большая продолжительность приема, особенно при большом числе направлений; повышенные требования к качеству геодезических сигналов; необходимость примерно одинаковой видимости по всем направлениям; разбивка направлений на группы при их большом числе на пункте; более высокая точность начального направления.

Способ измерения углов во всех направлениях – способ Шрейбера.Этот метод предложен Гауссом. Методика разработана Шрейбером, применившим его в 1870-х годах в прусской триангуляции. В России начал применяться с 1910 г., используется и в настоящее время. Суть способа: на пункте с n направлениями измеряют все углы, образующиеся при сочетании из n по 2, т.е.

1.2 1.3 1.4 … 1.n

2.3 2.4 … 2.n

3.4 … 3.n

… …

(n – 1)n

Число таких углов

.

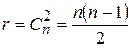Значение углов можно получить путем непосредственных измерений и путем вычислений. Если вес непосредственно измеренного угла равен 2 , то вес этого же угла, полученного из вычислений, будет равен 1. Следовательно. Вес угла, полученного из вычислений, в два раза меньше веса непосредственно измеренного угла.

При уравнивании на станции для каждого угла вычисляют его среднее значение из всех приемов (при допустимых расхождениях между приемами). Используя эти средние, находят уравненные на станции углы как среднее весовое значение. Учитывая, что сумма весов измеренного и вычисленных значений данного угла 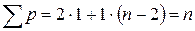, находим

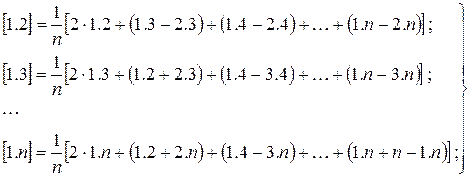
где n – число направлений на пункте. Углы, полученные в результате уравнивания на станции, по направлениям – равноточны.

Применяя формулу веса функции, для угла [1.2] находим

.

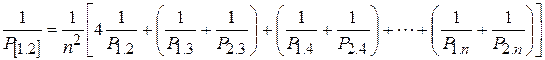Так как 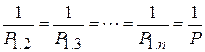, то 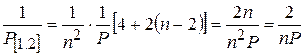, откуда 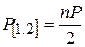. При Р = 1 , 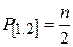, т.е. веса уравненных углов равны половине числа направлений, наблюдаемых с данного пункта. Если каждый угол измерен m приемами, то при n направлениях вес каждого угла будет равен mn / 2. Для равенства весов окончательных углов на всех станциях необходимо, чтобы произведение mn для всех пунктов сети являлось постоянным. Так как вес направления в два раза больше веса угла, то mn – вес направления.

Вес углов, измеренных во всех комбинациях должен быть равен весу углов, измеренных способом круговых приемов, т.е. p = m_кр = mn / 2 , откуда 2m_кр = mn , где m_кр – число приемов в методе круговых приемов. Например, если углы в триангуляции 2 класса измеряют 15 круговыми приемами (m_кр = 15), то mn = 30; при числе направлений n = 5 способом во всех комбинациях их нужно измерять 6 приемами (m = 30 / 5 = 6).

При измерении углов способом во всех комбинациях выполняют следующий контроль: 1) расхождение углов из двух полуприемов – 6” для теодолита с окулярным микрометром и 8” – без; 2) расхождение углов из разных приемов 4 и 5” для сетей 1 и 2 классов соответственно; 3) колебание среднего значения угла, полученного по результатам непосредственных измерений и найденного из вычислений, не должно превышать 3 “ при n до 5 и 4” – более 5. Если законченные приемы не удовлетворяют этим допускам, то их переделывают на тех же установках круга. Если второй контроль не выполняется, то перенаблюдают углы, имеющие максимальное и минимальное значение, при тех же установках круга. Все наблюдения выполняют заново, если число повторных приемов более 30% от числа приемов, предусмотренных программой. Наблюдения повторяют и при несоблюдении третьего контроля.

С.к.о. единицы веса и уравненного угла определяют по формулам

.

Достоинстваспособа: уравненные результаты являются рядом равноточных направлений; углы можно измерять в любой последовательности, выбирая наиболее благоприятные условия видимости и обеспечивая в итоге высокую точность; малая продолжительность одного приема (2-4 минуты измерения угла) обеспечивает меньшую зависимость точности результата от кручения сигнала; большое число перестановок горизонтального круга ослабляет влияние ошибок диаметров лимба.

Недостатки:быстрое уменьшение числа m приемов измеренного угла с ростом числа n направлений на пунктах (малое число приемов непосредственного измерения углов снижает точность их средних и уравненных значений); быстрый рост объема работ при n > 5.

Способ неполных приемовпредложен в 1954 г. Ю.А. Аладжаловым. Все направления разбивают на группы по три направления (без замыкания горизонта) так, чтобы определяемые по ним углы соответствовали бы углам, измеренным во всех комбинациях, но требовали бы меньшего объема работ и позволили увеличить число приемов непосредственных измерений каждой группы направлений. Следовательно, в этом способе заложено стремление избавиться от недостатков методов Струве и Шрейбера при наблюдении на пунктах с большим количеством направлений.

Практически не всегда путем подбора можно разбить направления на группы из трех направлений. В этом случае кроме групп из трех направлений измеряют отдельные углы, дополняющие программу. Программа измерений приведена в Инструкции. Способ неполных приемов применяется в триангуляции 2 класса на пунктах с 7 – 9 направлениями.

Обработка результатов измерений на станции заключается в определении средних значений направлений из m приемов в каждой группе и средних значений отдельных углов. По этим средним значениям вычисляют все углы – по три угла из каждой группы из трех направлений. Окончательно уравненные углы вычисляют по формулам способа Шрейбера. С.к.о. уравненных направлений определяют по формуле

,

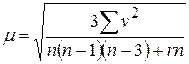где v – разности между измеренными и уравненными значениями углов; n – число направлений на пункте; r – число отдельно измеренных углов в программе. Вес уравненных направлений

,

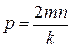где m – число приемов измерений направлений и отдельных углов; n, k – число направлений на пункте и в группе соответственно (k = 3, для углов k = 2).

Достоинства способа: результаты уравнивания на станции равноточны; объем работы на пункте на 20 – 25% меньше, чем в способе Шрейбера; число приемов непосредственных измерений групп при n = 7 – 9 больше, чем в способе Шрейбера, что позволяет более полно ослаблять ошибки измерений; дает возможность измерять направления, на которые в данный момент имеется хорошая видимость; короткая продолжительность приема (2 – 4 минуты), что позволяет уменьшить зависимость точности измерений от качества сигнала.

Недостатки:отсутствуют правила образования групп из трех направлений; при n = 8 нужно измерять большое число отдельных углов, что приводит к неклторому нарушению равноточности уравненных направлений; программа не предусматривает ослабление односторонне действующих ошибок измерений.

Видоизмененный способ измерения углов в комбинацияхпредложен А.Ф.Томилиным. Используется в триангуляции 2 класса на пунктах с 6 – 9 направлениями. В этом способе на станции с n направлениями независимо измеряют 2n углов:

1.2 2.3 3.4 … n.1;

1.3 2.4 3.5 … n.2.

Каждый угол измеряют 5 или 6 приемами. В этом способе измеряют не все углы, образующие сочетания направлений из n по 2, поэтому результат уравнивания на станции не является рядом равноточных направлений, и формулы для вычислений поправок в измеренные углы являются довольно сложными.

Достоинстваспособа: при n =7 – 9 число приемов непосредственных из

Дата добавления: 2014-03-24; просмотров: 1192; Нарушение авторских прав

Мы поможем в написании ваших работ!