Алгоритм расчета теплопередачи через непроницаемые стенки

Рассматривают две постановки задачи расчета теплопередачи: прямую и обратную. Прямая задача расчета теплопередачи ставит своей целью расчет температурного поля и теплового потока через стенку при известных геометрических и теплофизических параметрах. В этом случае для расчета также необходимо знать две любые температуры в расчетной области теплообмена и, если необходимо рассчитывать температуру флюидов, то и коэффициенты теплоотдачи.

Результатом решения обратной задачи расчета теплопередачи является определение одного из параметров однозначности: толщины стенки – δ, коэффициента теплопроводности материала стенки – λ, коэффициентов теплоотдачи 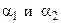. Для решения обратной задачи теплопередачи должны быть заданы две температуры в рассматриваемой расчетной области и тепловой поток или удельный тепловой поток

Алгоритм решения прямой задачи

1. На первом этапе решения прямой задачи необходимо рассчитать термические сопротивления всех элементарных участков теплопередачи:

— теплоотдачи от горячего флюида к стенке;

— теплопроводности всех слоев стенки;

— теплоотдачи от стенки к холодному флюиду.

2. Затем по формуле теплопередачи определяют поверхностную плотность теплового потока (q) или линейную плотность теплового потока (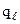) по двум заданным температурам и термическому сопротивлению участка между этими температурами:

; ,

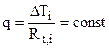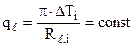где 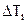– перепад температур на заданном участке теплообмена; 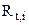и 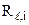– термические сопротивления плоской и цилиндрической стенок на участке теплообмена между заданными температурами.

3. На третьем этапе расчета теплопередачи находят неизвестные температуры в расчетной области теплопередачи. Для этого выбирают участок теплообмена таким образом, чтобы на одной из его границ была известная температура, а на другой – искомая. Затем по основной формуле теплопередачи находят неизвестную температуру, предварительно рассчитав термическое сопротивление данного участка.

Алгоритм решения обратной задачи

1. При решении обратной задачи тепловой поток или удельный тепловой поток – заданная по условию величина. Поэтому сразу находят термическое сопротивление участка теплообмена между заданными температурами:

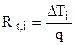; или ,

где 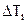– перепад температур на заданном участке теплообмена; 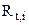и 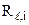– термические сопротивления плоской и цилиндрической стенок на участке теплообмена между заданными температурами.

2. На втором этапе решения обратной задачи (в зависимости от целей расчета) по известному термическому сопротивлению находят один из параметров однозначности: толщину слоя стенки – δ, коэффициент теплопроводности материала стенки – λ, либо один из коэффициентов теплоотдачи .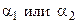

3. Если по условию задачи требуется рассчитать неизвестные температуры в заданной расчетной области теплопередачи, то необходимо выполнить пункты 1 и 3 алгоритма решения прямой задачи.

Дата добавления: 2014-03-11; просмотров: 800; Нарушение авторских прав

Мы поможем в написании ваших работ!