Бесконечно малые и бесконечно большие функции

Функция a(x) называется бесконечно малой (большой) в точке a, если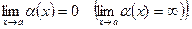

Свойства бесконечно малых и бесконечно больших функций.

1. 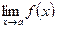существует и равен A тогда и только тогда, когда f(x)=A+a(x), где a(x)-бесконечно малая функция в точке a.

2. Сумма и произведение конечного числа бесконечно малых в точке a функций, а также произведение бесконечно малой в точке a функции на ограниченную функцию является бесконечно малыми в точке a функциями.

3. Если a(x) – бесконечно малая в точке a, то функция 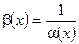- бесконечно большая в точке a и наоборот.

Сравнение бесконечно малых функций по порядку малости.

Пусть даны две бесконечно малые в точке a функции a(x) и b(x). Тогда если 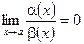, то a(x) – бесконечно малая более высокого порядка малости (обозначение: a(x)=0(b(x)); если 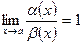, то a(x) и b(x) эквивалентны 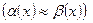; если , то a(x) и b(x) – бесконечно малые одного порядка малости; если 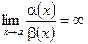, то a(x) – бесконечно малая более низкого порядка малости, чем b(x).

Дата добавления: 2014-11-08; просмотров: 556; Нарушение авторских прав

Мы поможем в написании ваших работ!