
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Свойства пределов функций
1. Функция не может иметь более одного предела.
2. Если у функции в заданной точке существует конечный предел, то в некоторой проколотой окрестности этой точки функция ограничена.
3. Если функция в заданной точке имеет конечный, но не равный нулю предел, то в некоторой проколотой окрестности этой точки функция имеет тот же знак, что и указанный предел (в частности, она не равна нулю).
4. Если 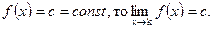
5. Если 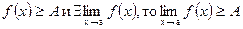
6. Если 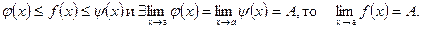
7. Если существуют конечные пределы 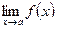 и
и 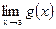 , то существуют и конечные пределы
, то существуют и конечные пределы 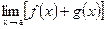 ,
, 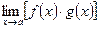 , а если
, а если 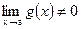 , то и
, то и 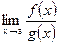 и, причем
и, причем 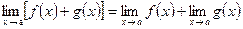 ;
; 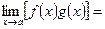
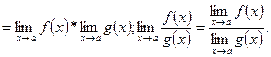
Следствие. Если существует 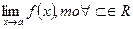
Замечательные пределы.
1. 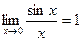
2. 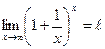 . Введя замену
. Введя замену  и заметив, что при
и заметив, что при 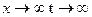 , получим другой вид второго замечательного предела:
, получим другой вид второго замечательного предела: 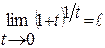
| <== предыдущая страница | | | следующая страница ==> |
| Предел функции. Непрерывность функции. Символ «о» малое | | | Бесконечно малые и бесконечно большие функции |
Дата добавления: 2014-11-08; просмотров: 359; Нарушение авторских прав

Мы поможем в написании ваших работ!