
Главная страница Случайная лекция

Мы поможем в написании ваших работ!
Порталы:
БиологияВойнаГеографияИнформатикаИскусствоИсторияКультураЛингвистикаМатематикаМедицинаОхрана трудаПолитикаПравоПсихологияРелигияТехникаФизикаФилософияЭкономика

Мы поможем в написании ваших работ!
Предел функции. Непрерывность функции. Символ «о» малое
План лекции
1. Определения предела, геометрическая интерпретация определения.
2. Определения односторонних пределов функции, геометрический смысл этих понятий.
3. Свойства пределов функций.
4. Первый и второй замечательные пределы.
5. Бесконечно малые и бесконечно большие функции, их свойства. Связь предела функции с бесконечно малой функцией.
6. Сравнение бесконечно малых функций по порядку малости. Символ «о» и его свойства.
7. Асимптотические формулы для простейших элементарных функций.
8. Свойства непрерывных функций.
9. Виды точек разрыва.
Определение предела функции
Пусть функция f определена на некоторой проколотой окрестности  точки
точки 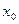 (т.е. окрестности точки
(т.е. окрестности точки 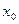 , исключая саму эту точку). Число A называется пределом функции f в точке
, исключая саму эту точку). Число A называется пределом функции f в точке 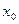 , если
, если 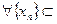
 ,
, 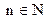 , сходящей к точке
, сходящей к точке 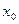 :
: 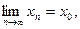 последовательность
последовательность 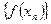 сходится к числу A, т.е. верно равенство:
сходится к числу A, т.е. верно равенство: 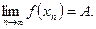 Обозначение:
Обозначение: 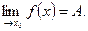
Для любого сколь угодно малого e > 0 найдется d > 0, такое, что для любой числовой последовательности 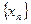 , все члены которой, начиная с некоторого номера
, все члены которой, начиная с некоторого номера 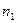 , расположены в проколотой d-окрестности точки
, расположены в проколотой d-окрестности точки 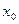 , соответствующие значения последовательности
, соответствующие значения последовательности 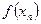 :
: 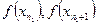 , ... попадут в e-окрестность точки A.
, ... попадут в e-окрестность точки A.
Определение предела функции
Число A называется пределом функции f в точке 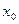 , если
, если  e >0 $ d >0 :
e >0 $ d >0 : 
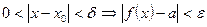
Для любой сколь угодно малой e-окрестности точки A существует такая проколотая окрестность точки 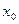 , что для любых x из этой окрестности, соответствующие значения функции f (x) попадут в e-окрестность точки A.
, что для любых x из этой окрестности, соответствующие значения функции f (x) попадут в e-окрестность точки A.
Односторонние пределы.
Определение Пусть функция f определена на интервале 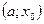 (соответственно на интервале
(соответственно на интервале 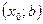 ). Число A называется пределом слева (справа) функции f в точке
). Число A называется пределом слева (справа) функции f в точке 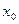 , если какова бы ни была такая
, если какова бы ни была такая 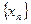 , что
, что 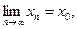
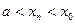
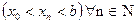 , последовательность
, последовательность 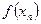 сходится к числу b, т.е.
сходится к числу b, т.е. 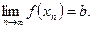 Обозначения:
Обозначения: 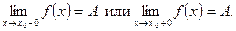
Геометрический смысл: для любого сколь угодно малого e > 0 найдется d > 0, такое, что для любой числовой последовательности, все члены которой, начиная с некоторого номера 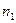 , находятся в интервале
, находятся в интервале 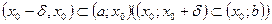 соответствующие значения последовательности
соответствующие значения последовательности 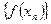 будут находиться в e-окрестности точки A.
будут находиться в e-окрестности точки A.
Определение одностороннего предела. Пусть функция f(x) определена на интервале 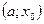 (соответственно на интервале
(соответственно на интервале 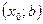 ). Число A называется пределом слева (справа) функции f(x) в точке
). Число A называется пределом слева (справа) функции f(x) в точке 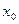 , если
, если 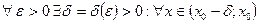 соответственно
соответственно 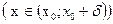 выполняется неравенство
выполняется неравенство 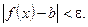
Для любой сколь угодно малой e-окрестности точки b найдется d>0, такое, что 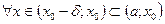
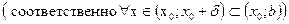 соответствующие значения функции f(x) попадут в e-окрестность точки b.
соответствующие значения функции f(x) попадут в e-окрестность точки b.
Теорема. Функция f(x) имеет предел в точке 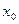 тогда и только тогда, когда в этой точке существуют пределы как справа, так и слева, и они равны. В этом случае их общее значение и является пределом функции f в точке
тогда и только тогда, когда в этой точке существуют пределы как справа, так и слева, и они равны. В этом случае их общее значение и является пределом функции f в точке 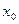 :
:
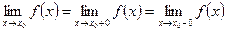
| <== предыдущая страница | | | следующая страница ==> |
| Царство животных | | | Свойства пределов функций |
Дата добавления: 2014-11-08; просмотров: 582; Нарушение авторских прав

Мы поможем в написании ваших работ!