Свойства символа «о»

о(b)±о(b)=о(b) о(сb)=о(b) "с¹0 с(о(b))=о(b)

о(о(b))=о(b) о(b+о(b))=о(b) Если a~b , то a-b=о(a)=о(b).

Асимптотические формулы для простейших элементарных функций.

При a®0:

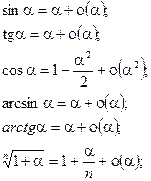
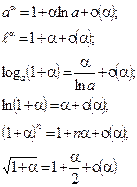
Непрерывность функции.

Функция f(x), определенная в некоторой окрестности точки 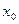, называется непрерывной в этой точке, если 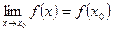. Это условие можно переписать в виде: 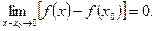Разность 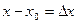называется приращением аргумента, а разность 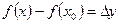называется приращением функции, соответствующим приращению аргумента Dx.

Тогда в этих обозначениях условие непрерывности функции запишется в виде: 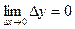, то есть бесконечно малому приращению аргумента соответствует бесконечно малое приращение функции.

Функция y=f(x) называется непрерывной на промежутке X, если она непрерывна в каждой точке этого промежутка.

Свойства непрерывных функций.

1. Все элементарные функции непрерывны в каждой точке своей области определения.

2. Если функции f и g непрерывны в точке 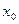, то функции cf (c=const), f+g, fg, а если, кроме того, 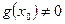, то и функция 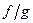также непрерывна в точке .

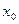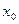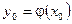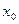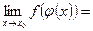
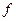
3. Пусть функция y=j(x) непрерывна в точке , а функция f(y) непрерывна в точке , тогда сложная функция f(j(x)) непрерывна в точке , то есть 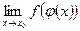. Говорят, что операция предельного перехода перестановочна с операцией взятия непрерывной функции.

Дата добавления: 2014-11-08; просмотров: 376; Нарушение авторских прав

Мы поможем в написании ваших работ!