Выравнивание статистического закона распределения случайной величины Т

На практике число опытов п ограничено, и статистический закон распределения является каким-то приближением к теоретическому (истинному) закону распределения случайной величины Т. Стремятся подобрать такую теоретическую кривую, которая бы отражала существенные черты статистического закона распределения и не отражала бы случайностей из-за малого количества данных. Вид закона распределения подбирают из существа задачи, либо но внешнему виду статистического закона распределения.

Будем аппроксимировать статистический закон распределения случайной величины Т экспоненциальным законом распределения f(t).

Для экспоненциального закона распределения имеем

;

.

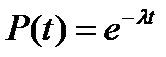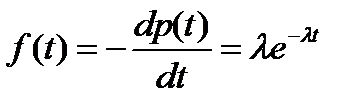Нужно определить параметры выбранного закона распределения.Выбранный экспоненциальный закон распределения зависит от одногопараметра 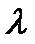. Оценку параметра 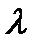обозначим через 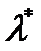. Оценку 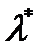мыопределяем из результатов опытов.

Используем для определения 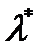метод моментов; приравниваемтеоретические и статистические моменты данного закона распределения.Имеем

.

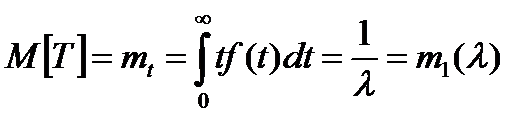Здесь - первый теоретический момент. По результатам опытовопределяем статистический первый момент 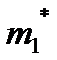. Имеем

;

где 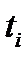- время безотказной работы i- го изделия; n - число опытов или число изделий, поставленных на испытания. Приравниваем эти моменты

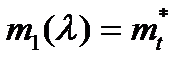
или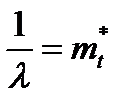

откуда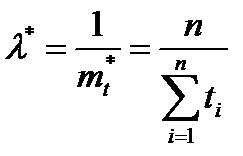

Пример 2: из результатов опытов определим , i =1, 2,…,k.

Будем аппроксимировать статистический закон распределенияслучайной величины Т нормальным законом распределения f(t) вида

Нужно определить параметры выбранного закона распределения.Выбранный нормальный закон распределения зависит от двух параметров 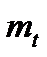и 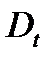. Определим оценк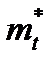и и 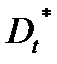этих параметров из результатов опытов.Используем для определения 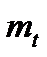и 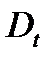метод моментов. Теоретическиемоменты закона распределения случайной величины Т:

начальные моменты порядка S определяются соотношением

;S=1,2, ……;

центральные моменты порядка S определяются формулой

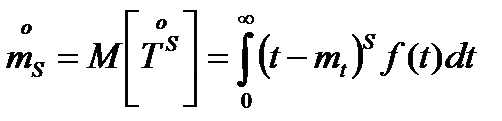;S=1,2, ……;

Здесь .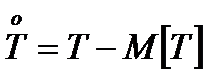

Определим 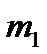и 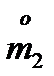( 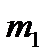- начальный момент 1 - го порядка; 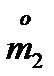-центральный момент 2-го порядка). Имеем:

;

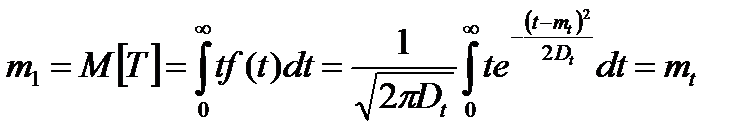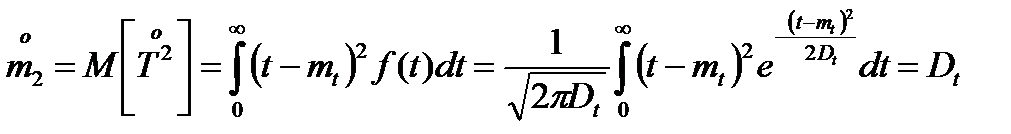
Таким образом ;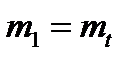

;

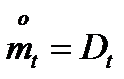Пo результатам опытов определяем статистические моменты и .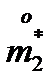

Имеем: ;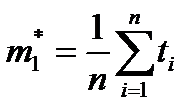

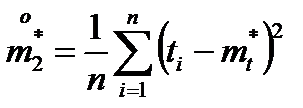
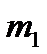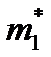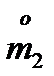Приравниваем и , и 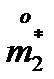; Имеем

, ;

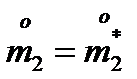или , .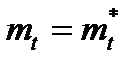

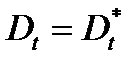Следовательно ;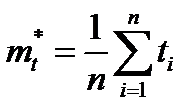

.

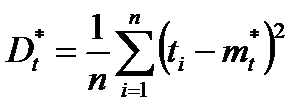Для оценкистепенирасхождениястатистическогозаконараспределения с теоретическим законом распределения выбираем мерурасхождения, по величине которой можно судить о том, вызвано лирасхождение случайными причинами, или разница между распределенияминастолько велика, что выбранный теоретический закон распределениянепригоден.

Обозначим меру расхождения через , которая может быть выбранаразличными способами.

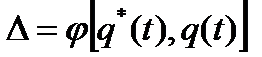, где 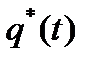– статистическаяфункцияраспределенияслучайной Т ;q(t) - функция распределения случайной величины Т.

Например:

;

;

;

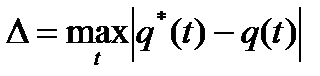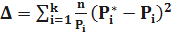где 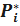- частота случайной величины T в интервал 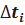, 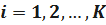; P_i– вероятность попадания случайной величины T в интервал , .

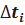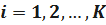Чем меньше , тем лучше согласуется статистический закон распределения с теоретическим законом распределения.

Выдвигаем гипотезу Hо том, что выбранный нами закон распределения случайно величины Tне противоречит статистическому закону распределения. На основании имеющегося статистического материала следует проверить эту гипотезу H. Широко используется два критерия проверки гипотезы H: критерий Пирсона и критерий Колмогорова.

Дата добавления: 2014-08-09; просмотров: 618; Нарушение авторских прав

Мы поможем в написании ваших работ!